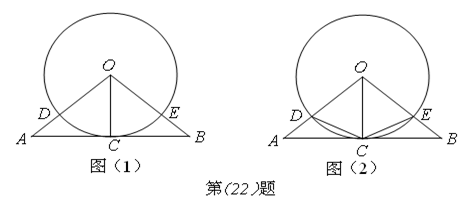
问题提出:平面内不在同一条直线上的三点确定一个圆.那么平面内的四点(任意三点均不在同一直线上),能否在同一个圆呢?
初步思考:设不在同一条直线上的三点A、B、C确定的圆为⊙O.
⑴当C、D在线段AB的同侧时,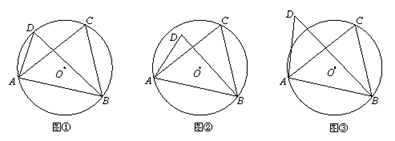
如图①,若点D在⊙O上,此时有∠ACB=∠ADB,理由是 ;
如图②,若点D在⊙O内,此时有∠ACB ∠ADB;
如图③,若点D在⊙O外,此时有∠ACB ∠ADB.(填“=”、“>”或“<”);
由上面的探究,请直接写出A、B、C、D四点在同一个圆上的条件: .
类比学习:(2)仿照上面的探究思路,请探究:当C、D在线段AB的异侧时的情形.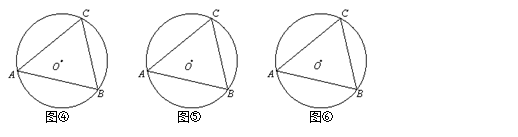
如图④,此时有 ,
如图⑤,此时有 ,
如图⑥,此时有 .
由上面的探究,请用文字语言直接写出A、B、C、D四点在同一个圆上的条件:
.
拓展延伸:(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
已知:如图,AB是⊙O的直径,点C在⊙O上.
求作:CN⊥AB.
作法:①连接CA, CB;
②在 上任取异于B、C的一点D,连接DA,DB;
上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB于M;
⑤连接D、M并延长,交⊙O于N.连接CN. 则CN⊥AB.
请按上述作法在图④中作图,并说明CN⊥AB的理由.(提示:可以利用(2)中的结论)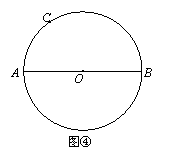
(本题4分)右图是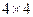 的正方形网格,请在其中选取一个白色的单位正方形并涂黑,使图中黑色部分是一个中心对称图形.
的正方形网格,请在其中选取一个白色的单位正方形并涂黑,使图中黑色部分是一个中心对称图形.
已知:如图①,四边形 是正方形,
是正方形, 是等边三角形,
是等边三角形, 为对角线
为对角线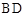 (不含
(不含 点)上任意一点,将
点)上任意一点,将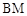 绕点
绕点 逆时针旋转
逆时针旋转 得到
得到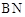 ,连接
,连接 、
、 、
、 。
。
(I)求证:
(II)①当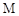 点在何处时,
点在何处时, 的值最小;
的值最小;
②当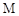 点在何处时,
点在何处时, 的值最小,并说明理由;
的值最小,并说明理由;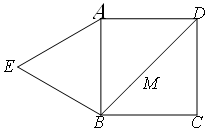
(III)当 的最小值为
的最小值为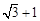 时,求正方形的边长。
时,求正方形的边长。
如图, 中,
中,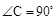 ,⊙O为它的内切圆,切点分别是
,⊙O为它的内切圆,切点分别是 、
、 、
、 。
。
(I)若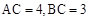 ,求:
,求: 的内切圆的半径;
的内切圆的半径;
(II)若 的内切圆半径
的内切圆半径 ,
, 的周长为
的周长为 ,则
,则 的值为
的值为
(III)若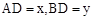 ,求
,求 。
。
如图所示,要设计一座1m高的抽象人物雕塑,使雕塑的上部(腰以上)AC与下部(腰以下)BC的高度比,等于下部与全部(全身)AB的高度比,雕塑的下部应设计为多高?
已知AB与⊙O相切于点C,OA=OB,OA,OB与⊙O分别交予点D,E
(I)如图①,若⊙O的直径为8,AB=10,求OA得长(结果保留根号);
(II)如图②,连接CD,CE,若四边形ODCE为菱形,求 的值。
的值。