如图，在平面直角坐标系中，直线
与抛物线
交于A、B两点，点A在x轴上，点B的横坐标为－8．
（1）求该抛物线的解析式；
（2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E．
①设△PDE的周长为l，点P的横坐标为x，求l关于x的函数关系式，并求出l的最大值；
②连接PA，以PA为边作图示一侧的正方形APFG．随着点P的运动，正方形的大小、位置也随之改变．当顶点F或G恰好落在y轴上时，直接写出对应的点P的坐标．
用适当的方法解下列方程
（1）
（2）
（3）
（4）
如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系．已知OA＝3，OC＝2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．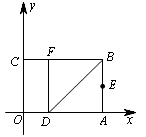
（1）直接写出点E、F的坐标；
（2）在y轴上是否存在点M，使得三角形MFE的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由．
（3）设顶点为F的抛物线交y轴正半轴于点P，且以点E、F、P为顶点的三角形是等腰三角形，求该抛物线的解析式；若顶点为F的抛物线交y轴负半轴于点P，且以点E、F、P为顶点的三角形是等腰三角形， 请直接写出点P的坐标．
制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为y（℃），从加热开始计算的时间为x（分钟）．据了解，设该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系（如图）．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．
（1）分别求出将材料加热和停止加热进行操作时，y与x的函数关系式；
（2）根据工艺要求，当材料的温度低于20℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？
如图，以△ABC的边AB为直径作⊙O，交BC于D点，交AC于E点，BD=DE．
（1）求证：△ABC是等腰三角形
（2）若E是AC的中点，求弧BD的度数．
如图，已知矩形ABCD中，AB＝1cm，BC＝2cm，以B为圆心，BC为半径作
圆弧交AD于F，交BA的延长线于E，求扇形BCE被矩形所截剩余部分的面积．