已知10m=3,10n=2,试求102m﹣n的值.
如图:网格中的每一个小正方形的边长是1,在这个网格中画一个钝角 ,使
,使 .(注:点C必须在格点上)
.(注:点C必须在格点上) 
如图,在△ABC中,AB=BC,点E在边AB上,EF⊥AC于F.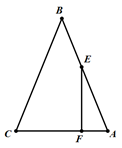
(1)尺规作图:过点A作AD⊥BC于点D(保留作图痕迹,不写作法);
(2)求证:∠CAD=∠AEF;
(3)若∠ABC=45°,AD与EF交于点G,求证:EG=2AF.
分解因式:
(1)(2a+1)2-(2a+1)(-1+2a)
(2)4(x+y)2-(x-y)2
计算:
(1) .
.
(2) .
.
(3) .
.
(4) .
.
在兰州市开展的“体育、艺术2+1”活动中,某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图甲、乙所示的条形统计图和扇形统计图.请你结合图中的信息解答下列问题: 
(1)样本中喜欢B项目的人数百分比是,其所在扇形统计图中的圆心角的度数是;
(2)把条形统计图补充完整;
(3)已知该校有1000人,根据样本估计全校喜欢乒乓球的人数是多少?