已知3m=6,9n=2,求32m﹣4n+1的值.
已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)①若四边形AEPF的面积为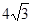 时,求x的值.
时,求x的值.
②四边形AEPF的面积是否存在最大值?若存在,请求出面积的最大值及此时x的值;若不存在,请说明理由.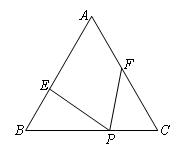
某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.图①中,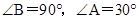 ;图②中,
;图②中, .图③是该同学所做的一个实验:他将△
.图③是该同学所做的一个实验:他将△ 的直角边
的直角边 与△
与△ 的斜边
的斜边 重合在一起,并将△
重合在一起,并将△ 沿
沿 方向移动.在移动过程中,
方向移动.在移动过程中, 两点始终在
两点始终在 边上(移动开始时点
边上(移动开始时点 与点
与点 重合).
重合).
(1) 在△ 沿
沿 方向移动的过程中,该同学发现:
方向移动的过程中,该同学发现: 两点间的距离;连接
两点间的距离;连接 的度数.(填“不变”、“ 逐渐变大”或“逐渐变小”)
的度数.(填“不变”、“ 逐渐变大”或“逐渐变小”)
(2) △ 在移动过程中,
在移动过程中, 与
与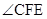 度数之和是否为定值,请加以说明;
度数之和是否为定值,请加以说明;
(3) 能否将△ 移动至某位置,使
移动至某位置,使 的连线与
的连线与 平行?如果能,请求出此时
平行?如果能,请求出此时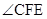 的度数,如果不能,请说明理由。
的度数,如果不能,请说明理由。
如图,在长方形 中,
中,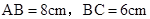 ,点
,点 是
是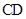 的中点,动点
的中点,动点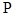 从
从 点出发,以每秒
点出发,以每秒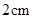 的速度沿
的速度沿 运动,最终到达点
运动,最终到达点 .若设点
.若设点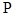 运动的时间是
运动的时间是 秒,那么当
秒,那么当 取何值时,△
取何值时,△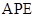 的面积会等于10 ?
的面积会等于10 ?
如图,在△ 中,
中, ,垂足为
,垂足为 ,点
,点 在
在 上,
上, ,垂足为
,垂足为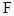 .
.
(1) 与
与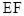 平行吗?为什么?
平行吗?为什么?
(2)如果 ,且
,且 ,求
,求 的度数.
的度数.
有一组等式: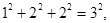
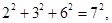
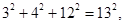
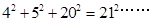 请观察它们的构成规律,用你发现的规律解答下面的问题:
请观察它们的构成规律,用你发现的规律解答下面的问题:
(1)写出第8个等式为;
(2)试用含正整数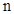 的等式表示你所发现的规律;
的等式表示你所发现的规律;
(3)说明你在(2)中所写等式成立的理由.