2014年阜宁县中小学积极开展体艺“2+1”活动,某校学生会准备调查八年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数:
(1)确定调查方式时,甲同学说:“我到八年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到八年级每个班随机调查一定数量的同学”。请你指出哪位同学的调查方式最合理;
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图。
| 类别 |
频数(人数) |
频率 |
| 武术类 |
25 |
0.25 |
| 书画类 |
20 |
0.20 |
| 棋牌类 |
15 |
 |
| 器乐类 |
 |
0.40 |
| 合计 |
 |
1.00 |

请你根据以上图表提供的信息解答下列问题:
①填空;a= , b= , c= ,
②在扇形统计图中器乐类所对应扇形的圆心角的度数是 ;
③若该校八年级有学生560人,请你估计大约有多少学生参加武术类校本课程.
如图,若将△ABC的绕点C顺时针旋转 90°后得到△DEC,则A点的对应点D的坐标是
,B点的对应点E的坐标是 ,请画出旋转后的△DEC(不要求写画法) .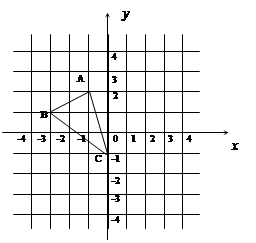
如图,AB是⊙O的弦,半径OC、OD分别交AB与点E、F,且AE=BF,请你找出线段OE、OF的数量关系,并给予证明.
解方程: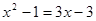
计算: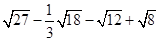
用甲.乙两种原料配制成某种饮料,已知这两种原料的维生素C的含量及购买这两种原料的价格如下表:
| 原料 维生素及价格 |
甲种原料 |
乙种原料 |
| 维生素C(单位/千克) |
600 |
100 |
| 原料价格(元/千克) |
8 |
4 |
(1)现配制这种饮料10千克,要求至少含有4200单位的维生素C,试写出所需甲种原料的质量x(千克)应满足的不等式.
(2)如果还要求购买甲.乙两种原料的费用不超过72元,那么你能写出x(千克)应满足的另一个不等式吗?