如图，107国道OA和320国道OB在我市相交于O点，在∠AOB的内部有工厂C和D，现要修建一个货站P，使P到OA,OB的距离相等且使PC=PD，用尺规作图法作出货站P的位置（不写作法，保留痕迹）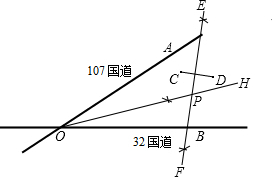
如图，在平面直角坐标系中，正方形OABC的边长为4，顶点A、C分别在x轴、y轴的正半轴，抛物线y=﹣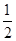 
x 2+bx+c经过B、C两点，点D为抛物线的顶点，连接AC、BD、CD．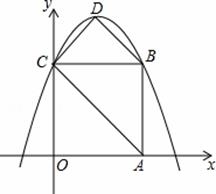 
（1）求此抛物线的解析式．
（2）求此抛物线顶点D的坐标和四边形ABDC的面积．
如图所示是甲乙两个工程队完成某项工程的进度图，首先是甲独做了10天，然后两队合做，完成剩下的工程．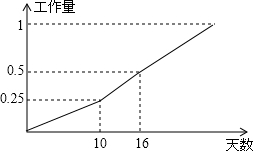 
（1）甲队单独完成这项工程，需要多少天？
（2）求乙队单独完成这项工程需要的天数；
（3）实际完成的时间比甲独做所需的时间提前多少天？
已知：关于x的一元二次方程mx 2-（3m+2）x+2m+2=0（m>0）．
（1）求证：方程有两个不相等的实数根；
（2）设方程的两个实数根分别为x 1，x 2（其中x 1< x 2）．若y是关于x的函数，且y=x 2-2x 1，求这个函数的解析式．
已知一个二次函数y=ax 2+bx+c的图象如图所示，请求出这个二次函数的解析式。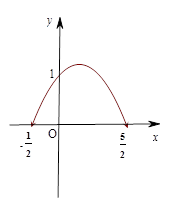 
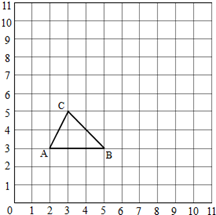
如图，不用量角器，在方格纸中画出△ABC绕点B顺时针方向旋转90°后得到的△A １BC １． 