如图,已知平面上有四个点A 、B、C、D.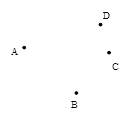
(1)连结AB,并画出AB的中点E;
(2)作射线AD;
(3)作直线BC与射线AD交于点F.
(浙江绍兴)课本中有一道作业题:
小颖解得此题的答案为48mm.小颖善于反思,她又提出了如下的问题.
(1)如果原题中所要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成的,如图,此时,这个矩形零件的两条边长又分别为多少mm?请你计算;
(2)如果原题中所要加工的零件只是一个矩形,如图,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
如图,王华在晚上由路灯A走向路灯B,当他走到点P时,发现身后的影子的顶部刚好接触到路灯A的底部;当他向前走12m到达Q时,发现身前他的影子的顶部刚好接触到路灯B的底部.已知王华的身高为1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离AB;
(2)当王华走到路灯B时,他在路灯A照射下的影长为多少?
阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不可到达),他们带了以下测量工具:皮尺、标杆、一副三角尺、小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.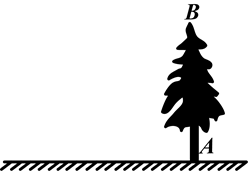
(1)所需的测量工具是________;
(2)请在图中画出测量示意图;
(3)设树AB的高度为x,请用所测数据(用小写字母表示)求出x.
一天晚上,李明和张龙利用灯光下的影子来测量一路灯D的高度,如图,当李明走到点A处时,张龙测得李明直立身高AM与其影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25m,已知李明直立时的身高为1.75m,求路灯的高CD.(结果精确到0.1m)
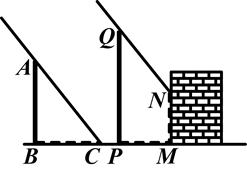
在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆AB=2米,它的影子BC=1.6米,木杆PQ的影子有一部分落在墙上,PM=1.2米,MN=0.8米,求木杆PQ的长度.