我们规定：函数
（a、b、k是常数，k≠ab）叫奇特函数．当a=b=0时，奇特函数就是反比例函数
（k是常数，k≠0）．
（1）如果某一矩形两边长分别是2和3，当它们分别增加x和y后，得到新矩形的面积为8．求y与x之间的函数表达式，并判断它是否为奇特函数；
（2）如图，在平面直角坐标系xOy中，矩形OABC的顶点A、C坐标分别为（6，0）、（0，3），点D是OA中点，连接OB、CD交于E，若奇特函数
的图象经过点B、E，求该奇特函数的表达式；
（3）把反比例函数
的图象向右平移4个单位，再向上平移 个单位就可得到（2）中得到的奇特函数的图象；
（4）在（2）的条件下，过线段BE中点M的一条直线l与这个奇特函数图象交于P，Q两点（P在Q右侧)，如果以B、E、P、Q为顶点组成的四边形面积为16，请直接写出点P的坐标． 
如图，在平面直角坐标系中，Rt△PBD的斜边PB落在y轴上，
tan∠BPD＝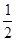
．延长BD交
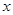轴于点C，过点D作DA⊥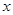轴，垂足为A，PD与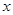轴交于点E，OA=8，OB=6．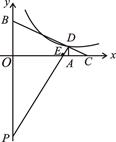
（1）求点C的坐标；
（2）若点D在反比例函数y =
（k＞0）的图象上，求反比例函数的解析式．
某海域有A、B、C三艘船正在捕鱼作业，C船突然出现故障，向A、B两船发出紧急求救信号，此时B船位于A船的北偏西47°方向，距A船26海里的海域，C船位于A船的北偏东58°方向，同时又位于B船的北偏东88°方向．
（1）求∠ABC的度数；
（2）A船以每小时40海里的速度前去救援，问多长时间能到出事地点．（结果精确到0．01小时）．
（参考数据：
≈1．414，
≈1．732）
某教研部门为了了解在校初中生阅读教科书的现状，随机抽取某校部分初中学生进行了调查，依据相关数据绘制成以下不完整的统计表，请根据图表中的信息解答下列问题：
某校初中生阅读教科书情况统计图表
| 类别 |
人数 |
占总人数比例 |
| 重视 |
a |
b |
| 一般 |
57 |
0．285 |
| 不重视 |
c |
0．36 |
| 说不清楚 |
9 |
0．045 |
（1）求样本容量及表格中a，b，c的值，并补全统计图；
（2）若该校共有初中生2500名，请估计该校“重视阅读教科书”的初中人数；
（3）①根据上面的统计结果，谈谈你对该校初中生阅读教科书的现状的看法及建议；
②如果要了解全省初中生阅读教科书的情况，你认为应该如何进行抽样？
（1）计算：（6．28－2π）0+（－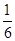
）－2－2cos60°；
（2）解方程：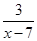
＝
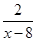
在直角坐标系
中，已知点P是反比例函数
（
＞0）图象上一个动点，以P为圆心的圆始终与
轴相切，设切点为A．
（1）如图1，⊙P运动到与轴相切，设切点为K，试判断四边形OKPA的形状，并说明理由．
（2）如图2，⊙P运动到与轴相交，设交点为B，C．当四边形ABCP是菱形时：
①求出点A，B，C的坐标．
②在过A，B，C三点的抛物线上是否存在点M，使△MBP的面积是菱形ABCP面积的
．若存在，试求出所有满足条件的M点的坐标，若不存在，试说明理由．
