在直角坐标系
中，已知点P是反比例函数
（
＞0）图象上一个动点，以P为圆心的圆始终与
轴相切，设切点为A．
（1）如图1，⊙P运动到与轴相切，设切点为K，试判断四边形OKPA的形状，并说明理由．
（2）如图2，⊙P运动到与轴相交，设交点为B，C．当四边形ABCP是菱形时：
①求出点A，B，C的坐标．
②在过A，B，C三点的抛物线上是否存在点M，使△MBP的面积是菱形ABCP面积的
．若存在，试求出所有满足条件的M点的坐标，若不存在，试说明理由．
甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同，每天甲、乙两人共加工35个零件，设甲每天加工x个.
（1）直接写出乙每天加工的零件个数（用含x的代数式表示）；
（2）求甲、乙每天各加工多少个零件；
“龟兔赛跑”是同学们熟悉的寓言故事。如图所示，表示了寓言中的龟、兔的路程S和时间t的关系（其中直线段表示乌龟，折线段表示兔子），请看图回答问题。
（1）赛跑中，兔子共睡了___________分钟；
（2）乌龟在这次比赛中的平均速度是__________米/分钟；
（3）乌龟比兔子早达到终点_________分钟；
（4）兔子醒来后赶到终点这段时间的平均速度是__________米/分钟。
解分式方程：
（1）化简：
；（2）化简并求值：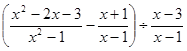
，其中x=－2．
如图，直角梯形OABC中，AB∥OC，O为坐标原点，点A在y轴正半轴上，点C在x轴正半轴上，点B坐标为（2，
），∠BCO=60°，OH⊥BC于点H．动点P从点H出发，沿线段HO向点O运动，动点Q从点O出发，沿线段OA向点A运动，两点同时出发，速度都为每秒1个单位长度．设点P运动的时间为t秒．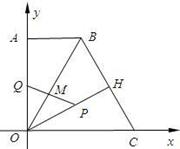
（1）求OH的长；
（2）若△OPQ的面积为S（平方单位）．求S与t之间的函数关系式．并求t为何值时，△OPQ的面积最大，最大值是多少；
（3）设PQ与OB交于点M．①当△OPM为等腰三角形时，求（2）中S的值．②探究线段OM长度的最大值是多少，直接写出结论．