(本小题满分14分)如图,在四棱柱 中,
中,
 底面
底面 ,
,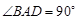 ,
, ,且
,且 ,点E在棱AB上,平面
,点E在棱AB上,平面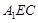 与棱
与棱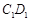 相交于点F.
相交于点F.
(Ⅰ)证明: ∥平面
∥平面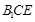 ;
;
(Ⅱ)若E是棱AB的中点,求二面角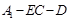 的余弦值;
的余弦值;
(Ⅲ)求三棱锥 的体积的最大值.
的体积的最大值.
已知集合A= ,B=
,B=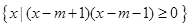 ,
,
(1)当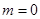 时,求
时,求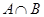
(2)若 :
: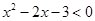 ,
,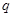 :
: ,且
,且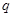 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围。
的取值范围。
甲,乙两人进行射击比赛,每人射击 次,他们命中的环数如下表:
次,他们命中的环数如下表:
| 甲 |
5 |
8 |
7 |
9 |
10 |
6 |
| 乙 |
6 |
7 |
4 |
10 |
9 |
9 |
(Ⅰ)根据上表中的数据,判断甲,乙两人谁发挥较稳定;
(Ⅱ)把甲6次射击命中的环数看成一个总体,用简单随机抽样方法从中抽取两次命中的环数组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过 的概率.
的概率.
在 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
,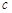 ,向量
,向量 ,
, ,且
,且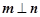 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,
, ,求
,求 的值.
的值.
已知 ,且
,且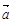 与
与 的夹角为120°.
的夹角为120°.
求:(1)  ; (2)
; (2) 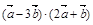 ; (3)
; (3)  .
.
已知 为第三象限角,
为第三象限角,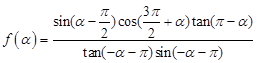 .
.
(1)化简 ;
;
(2)若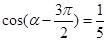 ,求
,求 的值.
的值.