(本小题满分13分)最近,张师傅和李师傅要将家中闲置资金进行投资理财. 现有两种投资方案,且一年后投资盈亏的情况如下:
(1)投资股市:
| 投资结果 |
获利 |
不赔不赚 |
亏损 |
| 概 率 |
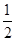 |
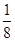 |
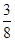 |
(2)购买基金:
| 投资结果 |
获利 |
不赔不赚 |
亏损 |
| 概 率 |
 |
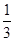 |
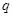 |
(Ⅰ)当 时,求q的值;
时,求q的值;
(Ⅱ)已知“购买基金”亏损的概率比“投资股市”亏损的概率小,求 的取值范围;
的取值范围;
(Ⅲ)已知张师傅和李师傅两人都选择了“购买基金”来进行投资,假设三种投资结果出现的可能性相同,求一年后他们两人中至少有一人获利的概率.
已知函数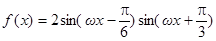 (其中
(其中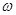 为正常数,
为正常数, )的最小正周期为
)的最小正周期为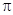 .
.
(1)求 的值;
的值;
(2)在△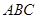 中,若
中,若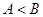 ,且
,且 ,求
,求 .
.
设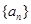 是公比
是公比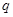 大于1的等比数列,
大于1的等比数列,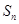 为数列
为数列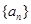 的前
的前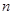 项和,已知
项和,已知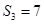 ,且
,且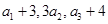 构成等差数列.
构成等差数列.
(1)求数列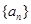 的通项公式;
的通项公式;
(2)令 ,求数列
,求数列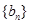 的前
的前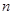 项和
项和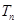 .
.
(本题满分12分)
已知函数 是实数集R上的奇函数,且
是实数集R上的奇函数,且 在R上为增函数。
在R上为增函数。
(Ⅰ)求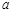 的值;
的值;
(Ⅱ)求 在
在 恒成立时的实数t的取值范围。
恒成立时的实数t的取值范围。
(本题满分12分)
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆右顶点到直线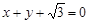 的距离为
的距离为 ,离心率
,离心率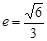
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知A为椭圆与y轴负半轴的交点,设直线 :
: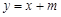 ,是否存在实数m,使直线
,是否存在实数m,使直线 与(Ⅰ)中的椭圆有两个不同的交点M、N,是∣AM∣=∣AN∣,若存在,求出 m的值;若不存在,请说明理由。
与(Ⅰ)中的椭圆有两个不同的交点M、N,是∣AM∣=∣AN∣,若存在,求出 m的值;若不存在,请说明理由。
(本题满分12分)
已知数列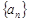 的前 n项和为
的前 n项和为 ,满足
,满足 ,且
,且 .
.
(Ⅰ)求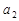 ,
, ;
;
(Ⅱ)若 ,求证:数列
,求证:数列 是等比数列。
是等比数列。
(Ⅲ)若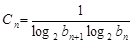 , 求数列
, 求数列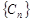 的前n项和
的前n项和 。
。