(本题满分12分)
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆右顶点到直线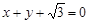 的距离为
的距离为 ,离心率
,离心率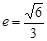
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知A为椭圆与y轴负半轴的交点,设直线 :
: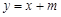 ,是否存在实数m,使直线
,是否存在实数m,使直线 与(Ⅰ)中的椭圆有两个不同的交点M、N,是∣AM∣=∣AN∣,若存在,求出 m的值;若不存在,请说明理由。
与(Ⅰ)中的椭圆有两个不同的交点M、N,是∣AM∣=∣AN∣,若存在,求出 m的值;若不存在,请说明理由。
(本小题16分)如图所示,数列 的前
的前 项的和
项的和 ,
, 为数列
为数列 的前
的前 项的和,且
项的和,且 .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)找出所有满足: 的自然数
的自然数 的值(不必证明);
的值(不必证明);
(3)若不等式 对于任意的
对于任意的 ,
, 恒成立,求实数
恒成立,求实数 的最小值,并求出此时相应的
的最小值,并求出此时相应的 的值.
的值.
(本小题14分)已知函数f(x)= ,x∈[1,+∞
,x∈[1,+∞
(1)当a= 时,求函数f(x)的最小值
时,求函数f(x)的最小值
(2)若对任意x∈[1,+∞ ,f(x)>0恒成立,试求实数a的取值范围
,f(x)>0恒成立,试求实数a的取值范围
(3)求f(x)的最小值
(本小题14分)某企业生产A、B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如左图, B产品的利润与投资的算术平方根成正比,其关系如右图 (注:利润与投资单位:万元).
(1)分别将A、B两种产品的利润表示为投资 (万元)的函数关系式;
(万元)的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元?
(本小题14分)已知函数f(x)= (x+
(x+ -a)的定义域为A,值域为B.
-a)的定义域为A,值域为B.
(1)当a=4时,求集合A;
(2)当B=R时,求实数a的取值范围.
(本小题满分16分)
已知函数 ,
, ,其中
,其中 ,
, ,且
,且 。
。
(1)若1是关于 的方程
的方程 的一个解,求
的一个解,求 的值;
的值;
(2)当 时,不等式
时,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(3)当 时,函数
时,函数 的最小值为
的最小值为 ,求
,求 的解析式.
的解析式.