(本小题16分)如图所示,数列 的前
的前 项的和
项的和 ,
, 为数列
为数列 的前
的前 项的和,且
项的和,且 .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)找出所有满足: 的自然数
的自然数 的值(不必证明);
的值(不必证明);
(3)若不等式 对于任意的
对于任意的 ,
, 恒成立,求实数
恒成立,求实数 的最小值,并求出此时相应的
的最小值,并求出此时相应的 的值.
的值.
某社团组织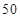 名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,倡导文明新风;2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下2
名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,倡导文明新风;2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下2 2的列联表所示:
2的列联表所示:
| 宣传慰问 |
义工 |
总计 |
|
| 20至40岁 |
16 |
||
| 大于40岁 |
15 |
23 |
|
| 总计 |
24 |
50 |
(1)填上表中所空缺的数值。
(2)分层抽样方法在做义工的志愿者中随机抽取6名,年龄在20至40岁与大于40岁的应该各抽取几名?
(3)根据(2)抽取的6名志愿者中任取2名,求选取的2人中分别来自上述年龄段各1人的概率。
已知复数z=1﹣i(i是虚数单位)
(Ⅰ)计算z2;
(Ⅱ)若z2+a ,求实数a,b的值.
,求实数a,b的值.
【原创】
(1)观察下列各式; 根据以上各式利用归纳推理得出一个一般性的结论;
根据以上各式利用归纳推理得出一个一般性的结论;
(2)设
 根据
根据 的大小关系证明(1)的结论;
的大小关系证明(1)的结论;
【改编】(本小题满分10分)已知函数 .
.
(1)求函数的单调增区间;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分10分)某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
| 分数段 |
[40,50) |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90,100] |
| 男 |
3 |
9 |
18 |
15 |
6 |
9 |
| 女 |
6 |
4 |
5 |
10 |
13 |
2 |
估计男、女生各自的成绩平均分(同一组数据用该组区间中点值作代表),从计算结果看,判断数学成绩与性别是否有关;
| 优分 |
非优分 |
合计 |
|
| 男生 |
|||
| 女生 |
|||
| 合计 |
100 |
(2)规定80分以上为优分(含80分),请你根据已知条件作出 列联表,并判断是否有
列联表,并判断是否有 以上的把握认为“数学成绩与性别有关”.
以上的把握认为“数学成绩与性别有关”.
附表及公式
 |
0.100 |
0.050 |
0.010 |
0.001 |
 |
2.706 |
3.841 |
6.635 |
10.828 |
 .
.