数列{an}满足:a1= , 前n项和Sn=
, 前n项和Sn=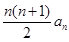 ,
,
(1)写出a2, a3, a4;(2)猜出an的表达式,并用数学归纳法证明.
设函数f(x)=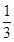 x3-ax(a>0),g(x)=bx2+2b﹣1.
x3-ax(a>0),g(x)=bx2+2b﹣1.
(1)若曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同的切线,求实数a,b的值;
(2)当b=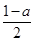 时,若函数h(x)=f(x)+g(x)在区间(﹣2,0)内恰有两个零点,求实数a的取值范围;
时,若函数h(x)=f(x)+g(x)在区间(﹣2,0)内恰有两个零点,求实数a的取值范围;
(3)当a=1,b=0时,求函数h(x)=f(x)+g(x)在区间[t,t+3]上的最小值.
已知椭圆(a>b>0)和直线l:y=bx+2,椭圆的离心率e= ,坐标原点到直线l的距离为
,坐标原点到直线l的距离为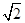 .
.
(1)求椭圆的方程;
(2)已知定点E(﹣1,0),若直线y=kx+2(k≠0)与椭圆相交于C,D两点,试判断是否存在实数k,使得以CD为直径的圆过定点E?若存在,求出k的值;若不存在,请说明理由.
已知{an}是等差数列,其前n项的和为Sn,{bn}是等比数列,且a1=b1=2,a4+b4=21,S4+b4=30.(1)求数列{an}和{bn}的通项公式;
(2)记cn=anbn,n∈N*,求数列{cn}的前n项和.
已知三棱柱ABC﹣A1B1C1的三视图及直观图如图所示,根据图中所给数据,解答下列问题: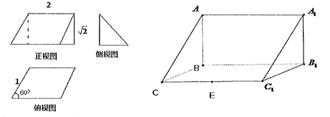
(1)求证:C1B⊥平面ABC;
(2)试在棱CC1(不包含端点C、C1)上确定一点E的位置,使得EA⊥EB1;
(3)求三棱柱ABC﹣A1B1C1的体积.
2014年“五一节”期间,高速公路车辆较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(km/h)分成七段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),[90,95)后得到如图所示的频率分布直方图,据图解答下列问题: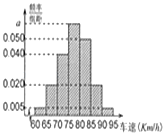
(1)求a的值,并说明交警部门采用的是什么抽样方法?
(2)求这120辆车行驶速度的众数和中位数的估计值(精确到0.1);
(3)若该路段的车速达到或超过90km/h即视为超速行驶,试根据样本估计该路段车辆超速行驶的概率.