选修4-4:坐标系与参数方程[(本小题满分10分)
己知直线  的参数方程为
的参数方程为 (t为参数),圆C的参数方程为
(t为参数),圆C的参数方程为 .(a>0.
.(a>0.  为参数),点P是圆C上的任意一点,若点P到直线
为参数),点P是圆C上的任意一点,若点P到直线 的距离的最大值为
的距离的最大值为 ,求a的值。
,求a的值。
(本小题满分l0分)选修4—5:不等式选讲
已知函数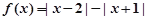 .
.
(Ⅰ)求证: ;
;
(Ⅱ)解不等式 .
.
(本小题共12分)
已知函数f(x)=2x-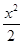 -aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
-aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
(2)求y=f(x)的极值点(即函数取到极值时点的横坐标).
(本小题满分12分)已知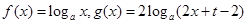
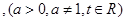 .
.
(1)当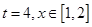 ,且
,且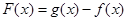 有最小值2时,求
有最小值2时,求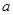 的值;
的值;
(2)当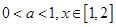 时,有
时,有 恒成立,求实数
恒成立,求实数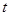 的取值范围.
的取值范围.
(本小题满分12分)已知函数y=f(x)= (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)< .试求函数f(x)的解析式
.试求函数f(x)的解析式
(本小题满分12分)已知函数 在点x=1处的切线与直线
在点x=1处的切线与直线 垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值.
垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值.