(本小题满分12分)已知函数y=f(x)= (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)< .试求函数f(x)的解析式
.试求函数f(x)的解析式
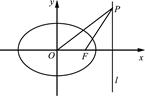
如图,在平面直角坐标系xOy中,椭圆C的中心在坐标原点O,右焦点为F.若C的右准线l的方程为x=4,离心率e=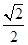 .
.
(1)求椭圆C的标准方程;
(2)设点P为准线l上一动点,且在x轴上方.圆M经过O、F、P三点,求当圆心M到x轴的距离最小时圆M的方程.
直线l过点(-4,0)且与圆(x+1)2+(y-2)2=25交于A,B两点,如果AB=8,求直线l的方程.
自点A(-3,3)发出的光线l射到x轴上,被x轴反射,反射光线所在的直线与圆C:x2+y2-4x-4y+7=0相切.求:
(1)光线l和反射光线所在的直线方程;
(2)光线自A到切点所经过的路程.
求半径为4,与圆x2+y2-4x-2y-4=0相切,且和直线y=0相切的圆的方程.
已知圆C:(x-3)2+(y-4)2=4,直线l1过定点A(1,0).
(1)若l1与圆相切,求l1的方程;
(2)若l1与圆相交于P、Q两点,线段PQ的中点为M,又l1与l2:x+2y+2=0的交点为N,判断AM·AN是否为定值?若是,则求出定值;若不是,请说明理由.