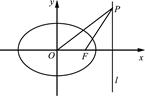
如图,在平面直角坐标系xOy中,椭圆C的中心在坐标原点O,右焦点为F.若C的右准线l的方程为x=4,离心率e=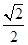 .
.
(1)求椭圆C的标准方程;
(2)设点P为准线l上一动点,且在x轴上方.圆M经过O、F、P三点,求当圆心M到x轴的距离最小时圆M的方程.
设椭圆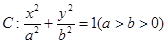 的左、右焦点分别为
的左、右焦点分别为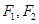 ,
,
上顶点为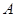 ,在
,在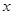 轴负半轴上有一点
轴负半轴上有一点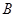 ,满足
,满足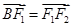 ,且
,且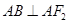 .
.
(Ⅰ)求椭圆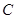 的离心率;
的离心率;
(Ⅱ)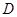 是过
是过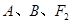 三点的圆上的点,
三点的圆上的点,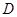 到直线
到直线 的最大距离等于椭圆长轴的长,求椭圆
的最大距离等于椭圆长轴的长,求椭圆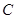 的方程;
的方程;
(Ⅲ)在(Ⅱ)的条件下,过右焦点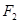 作斜率为
作斜率为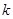 的直线
的直线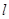 与椭圆
与椭圆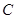 交于
交于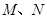 两点,线段
两点,线段 的中垂线与
的中垂线与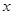 轴相交于点
轴相交于点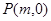 ,求实数
,求实数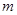 的取值范围.
的取值范围.
已知数列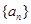 的前
的前 项和为
项和为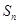 ,且
,且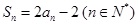 ,
,
数列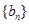 满足
满足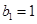 ,且点
,且点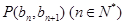 在直线
在直线 上.
上.
(Ⅰ)求数列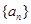 、
、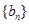 的通项公式;
的通项公式;
(Ⅱ)求数列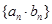 的前
的前 项和
项和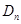 ;
;
(Ⅲ)设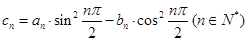 ,求数列
,求数列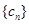 的前
的前 项和
项和 .
.
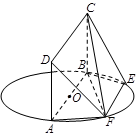
如图,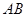 为圆
为圆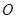 的直径,点
的直径,点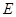 、
、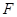 在圆
在圆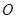 上,
上, ,矩形
,矩形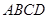 所在的平面与圆
所在的平面与圆 所在的平面互相垂直.已知
所在的平面互相垂直.已知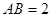 ,
,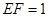 .
.
(Ⅰ)求证:平面 平面
平面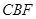 ;
;
(Ⅱ)求直线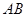 与平面
与平面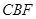 所成角的大小;
所成角的大小;
(Ⅲ)当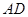 的长为何值时,平面
的长为何值时,平面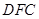 与平面
与平面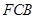 所成的锐二面角的大小为
所成的锐二面角的大小为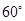 ?
?
给定直线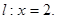 动圆M与定圆
动圆M与定圆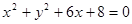 外切且与直线
外切且与直线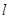 相切.
相切.
(1)求动圆圆心M的轨迹C的方程;
(2)设A、B是曲线C上两动点(异于坐标原点O),若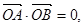 求证直线AB过一定点,并求出定点的坐标.
求证直线AB过一定点,并求出定点的坐标.
某学校为调查高二年级学生的身高情况,按随机抽样的方法抽取200名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有48人.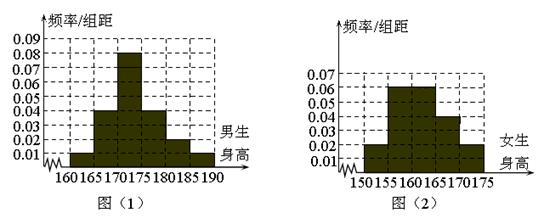 (Ⅰ)在抽取的学生中,身高不超过165cm的男、女生各有多少人?并估计男生的平均身高。
(Ⅰ)在抽取的学生中,身高不超过165cm的男、女生各有多少人?并估计男生的平均身高。
(Ⅱ)在上述200名学生中,从身高在170~175cm之间的学生按男、女性别分层抽样的方法,抽出7人,从这7人中选派4人当旗手,求4人中至少有一名女生的概率.