已知圆C:(x-3)2+(y-4)2=4,直线l1过定点A(1,0).
(1)若l1与圆相切,求l1的方程;
(2)若l1与圆相交于P、Q两点,线段PQ的中点为M,又l1与l2:x+2y+2=0的交点为N,判断AM·AN是否为定值?若是,则求出定值;若不是,请说明理由.
已知随机变量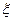 的概率分布列为分别求出随机变量η=
的概率分布列为分别求出随机变量η=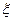 2的分布列.
2的分布列.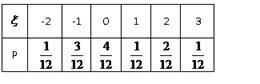
某电视台的一个智力游戏节目中,有一道将四本由不同作者所著的外国名著A、B、C、D与它们的作者连线的题目,每本名著只能与一名作者连线,每名作者也只能与一本名著连线.每连对一个得3分,连错得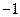 分,一名观众随意连线,他的得分记作ξ.
分,一名观众随意连线,他的得分记作ξ.
(1)求该观众得分ξ为非负的概率;
(2)求ξ的分布列及数学期望.
甲、乙两人破译一种密码,它们能破译的概率分别为 和
和 ,求:
,求:
(1)恰有一人能破译的概率;(2)至多有一人破译的概率;
(3)若要破译出的概率为不小于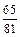 ,至少需要多少甲这样的人?
,至少需要多少甲这样的人?
甲、乙两人各射击一次,击中目标的概率分别是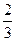 和
和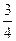 。假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响。
。假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响。
(Ⅰ)求甲射击4次,至少1次未击中目标的概率;
(Ⅱ)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(Ⅲ)假设两人连续两次未击中目标,则停止射击。问:乙恰好射击5次后,被中止射击的概率是多少?
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入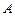 袋或
袋或 袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是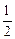 .
.
(Ⅰ)求小球落入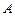 袋中的概率
袋中的概率 ;
;
(Ⅱ)在容器入口处依次放入4个小球,记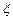 为落入
为落入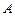 袋中的小球个数,试求
袋中的小球个数,试求 的概率和
的概率和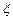 的数学期望
的数学期望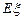 .
.