（本题满分14分，第1小题5分，第2小题9分）
一校办服装厂花费2万元购买某品牌运动装的生产与销售权，根据以往经验，每生产1百套这种品牌运动装的成本为1万元，每生产x（百套）的销售额R（x）
（万元）满足：
（1）该服装厂生产750套此种品牌运动装可获得利润多少万元？
（2）该服装厂生产多少套此种品牌运动装利润最大？此时，
利润是多少万元？
(本小题满分12分)
已知函数
，
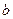为实数）有极值，且在
处的切线与直线
平行.
（I）求实数a的取值范围；
（II）是否存在实数a，使得函数
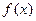的极小值为1，若存在，求出实数a的值；若不存
在，请说明理由；
（Ⅲ）设
求证：
.
(本小题满分12分)
已知函数
为奇函数，函数
在区间
上单调递减，在
上单调递增.
（I）求实数
的值；
（II）求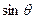
的值及
的解析式；
（Ⅲ）设
，试证：对任意的
且
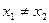都有
.
(本小题满分12分)
关于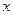
的函数
与数列
具有关系：
,
(
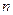=1,2,3,…)(
为常数)，又设函数的导数
，为方程
的实根.
（I）用数学归纳法证明：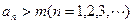
；
（II）证明：
.
(本小题满分12分)
试利用如图所示的等边三角形数阵，推导
(本小题满分12分)
已知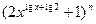
展开式中最后三项的系数的和是方程
的正数解，它的中间项是
，求
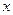的值．