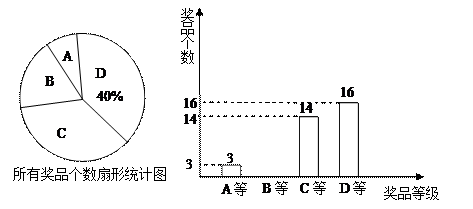
元旦晚会即将来临,小涵作为晚会主持人为本次晚会准备了A等,B等,C等,D等共
4类奖品,它们的价格可由下表表示 ,小涵绘制了如下两幅不完整的统计图:
 |
| 等级 |
价格(元/个) |
| A等 |
50 |
| B等 |
30 |
| C等 |
20 |
| D等 |
10 |
(1)小涵总共准备了__________个奖品,这些奖品平均每个的价格为__________元.
(2)补全条形统计图.
(3)在晚会的摸奖环节中,所有奖品均已发出,其中获得A等奖的有1位女同学,B等奖有4位女同学.现从获得A等和B等的同学中分别抽出一位做获奖感言,那么请你用画树状图或列表格的方法求出恰好有一位男同学和一位女同学做获奖感言的概率.
如图,在平面直角坐标系中,一次函数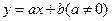 与x轴、
与x轴、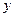 轴分别交于点C、
轴分别交于点C、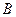 ,与反比例函数
,与反比例函数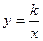 (k≠0)相交于A、D两点,其中BD=5,BO=2,
(k≠0)相交于A、D两点,其中BD=5,BO=2,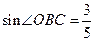 .
.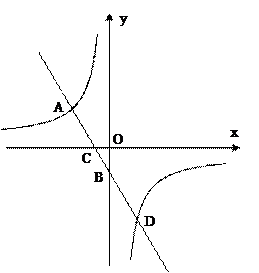
(1) 分别求出反比例函数和直线AB的解析式;
(2) 连接OD,求△COD的面积.
先化简,再求值: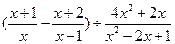 ,其中x满足方程
,其中x满足方程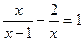 .
.
如果将抛物线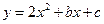 沿直角坐标平面先向左平移3个单位,再向下平移2个单位,得到了抛物线
沿直角坐标平面先向左平移3个单位,再向下平移2个单位,得到了抛物线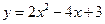 .
.
(1)试确定b,c的值;
(2)求出抛物线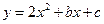 的对称轴和顶点坐标.
的对称轴和顶点坐标.
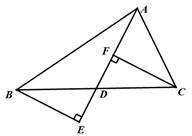
如图,在△ABC中,AD是BC边的中线,过点C、B分别作AD及其延长线的垂线CF、BE,垂足分别为点F、E.求证:BE=CF