已知:如图,AB是⊙O的直径,CD是⊙O的弦,且AB⊥CD,垂足为E.
(1)求证:∠CDB=∠A;
(2)若BD=5,AD=12,求CD的长.
(本题10分)如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.
(本题10分)如图,在平面直角坐标系xOy中,点A(−2,10),点B(6,10).
(1)只用直尺(没有刻度)和圆规,求作一个点P,使点P同时满足下列两个条件:
①点P到A,B两点的距离相等;②点P到两坐标轴的距离相等.(要求保留作图痕迹,不必写出作法)
(2)求出(1)中点P的坐标.
(本题10分)已知:等腰三角形的周长为80.
(1)写出底边长y与腰长x的函数表达式;
(2)当腰长为30时,底边长为多少?
(3)当底边长为8时,腰长为多少?
(本题8分)求下列各式中的x:
(1) ;
;
(2) .
.
(1)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.求∠DAE的度数.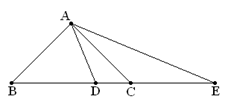
(2)如果把(1)题中的“AB=AC”的条件舍去,其余条件不变,那么∠DAE的度数会改变吗?并说明理由.
(3)如果把(1)题中“∠BAC=90°”的条件改为“∠BAC>90°”,其余条件不变,
那么∠DAE的度数与∠BAC有怎样的大小关系?并说明理由.