如图，在平面直角坐标系中，矩形OCDE的三个顶点分别是C（3，0），D（3，4），E（0，4）．点A在DE上，以A为顶点的抛物线过点C，且对称轴x=1交x轴于点B．连接EC，AC．点P，Q为动点，设运动时间为t秒．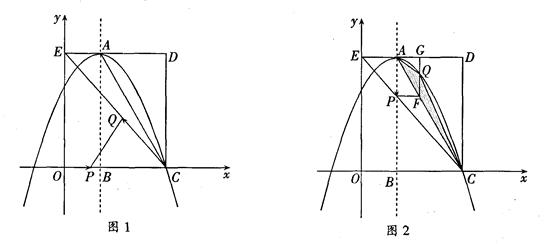
（1）填空：点A坐标为 ，抛物线的解析式为 ；
（2）在图1中，若点P在线段OC上从点O向点C以1个单位／秒的速度运动，同时，点Q在线段CE上从点C向E以2个单位／秒的速度运动，当一个点到达终点时，另一个点随之停止运动．连接PQ，是否存在实数t，使得PQ所在的直线经过点D，若存在，求出t的值；若不存在，请说明理由；
（3）在图2中，若点P在对称轴上从点A开始向点B以1个单位／秒的速度运动，过点P做PF⊥AB，交AC于点F，过点F作FG⊥AD于点G，交抛物线于点Q，连接AQ，CQ．当t为何值时，△ACQ的面积最大？最大值是多少？
分解因式：.
（1）
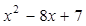（2）
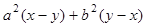
某商店经销一种销售成本为每千克40元的水产品，据市场分析，若每千克50元销售，一个月能售出500kg，销售单价每涨1元，月销售量就减少10kg，针对这种水产品情况，请解答以下问题：
（1）当月销售单价定为每千克55元时，计算月销售量和月销售利润．
（2）设销售单价为每千克x元，商店想在月销售成本不超过10000元的情况下，使得月销售利润达到8000元，求月销售单价应为多少?
如图，
是⊙O的直径， 点C在⊙O上，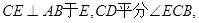
交过点B的射线于D,交AB于F,且
.
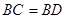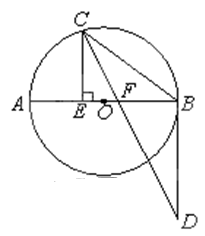
（1）求证：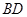
是⊙O的切线；（2）若
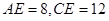, 求⊙O的半径.
已知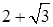
是方程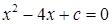
的一个根，求方程的另一个根及
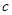的值。
如图，P是正方形ABCD内一点，连接PA、PB、PC，将△ABP绕点B顺时针旋转到△CBP′的位置．
（1）旋转中心是点 ，旋转的度数是 度；
（2）连结PP′，△BPP′的形状是 三角形；
（3）若PB＝4，求△BPP′的周长。