设偶函数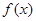 的定义域为R,当
的定义域为R,当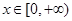 时,
时,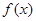 是增函数,则
是增函数,则 ,
, ,
,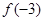 的大小关系是( )
的大小关系是( )
A. |
B. |
C. |
D. |
约束条件为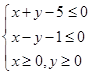 ,目标函数
,目标函数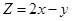 ,则
,则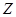 的最大值是
的最大值是
A.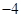 |
B.4 | C.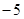 |
D.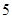 |
在空间中,下列命题正确的是
A.平面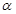 内的一条直线 内的一条直线 垂直与平面 垂直与平面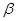 内的无数条直线,则 内的无数条直线,则 |
B.若直线 与平面 与平面 内的一条直线平行,则 内的一条直线平行,则 |
C.若平面 ,且 ,且 ,则过 ,则过 内一点 内一点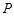 与 与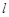 垂直的直线垂直于平面 垂直的直线垂直于平面 |
D.若直线 与平面 与平面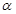 内的无数条直线都垂直,则不能说一定有 内的无数条直线都垂直,则不能说一定有 . . |
在等比数列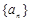 中,若公比
中,若公比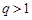 ,且
,且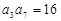 ,
,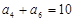 ,则
,则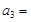
A.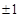 |
B.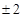 |
C.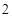 |
D.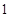 |
设非空集合P、Q满足 ,则
,则
A.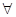 x x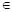 Q,有x Q,有x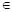 P P |
B.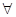  ,有 ,有 |
C.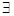 x0 x0 Q,使得x0 Q,使得x0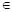 P P |
D.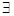 x0 x0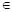 P,使得x0 P,使得x0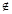 Q Q |
“回归”一词是在研究子女的身高与父母的身高之间的遗传关系时,由高尔顿提出的,他的研究结果是子代的平均身高向中心回归,根据他的结论,在儿子的身高y与父亲的身高x的回归方程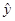 =a+bx中,b的取值
=a+bx中,b的取值
| A.在(-1,0)内 | B.等于0 | C.在(0,1)内 | D.在[1,+∞)内 |