(本小题满分14分)
如图,四边形 是正方形,△
是正方形,△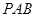 与△
与△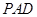 均是以
均是以 为直角顶点的等腰直角三角形,点
为直角顶点的等腰直角三角形,点 是
是 的中点,点
的中点,点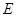 是边
是边 上的任意一点.
上的任意一点.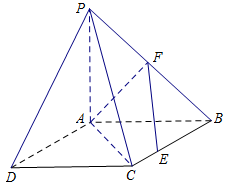
(1)求证: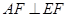 ;
;
(2)求二面角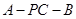 的平面角的正弦值.
的平面角的正弦值.
巳知椭圆 的离心率是
的离心率是 .
.
⑴若点P(2,1)在椭圆上,求椭圆的方程;
⑵若存在过点A(1,0)的直线 ,使点C(2,0)关于直线
,使点C(2,0)关于直线 的对称点在椭圆上,求椭圆的焦距的取值范围.
的对称点在椭圆上,求椭圆的焦距的取值范围.
定义在实数集上的函数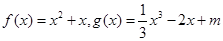 .
.
⑴求函数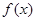 的图象在
的图象在 处的切线方程;
处的切线方程;
⑵若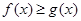 对任意的
对任意的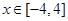 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
已知四棱锥P-ABCD中,PB⊥平面ABCD,底面ABCD是直角梯形,∠ABC=∠BCD=90°,PB=BC=CD= AB.Q是PC上的一点.
AB.Q是PC上的一点.
⑴求证:平面PAD⊥面PBD;
⑵当Q在什么位置时,PA∥平面QBD?
学校餐厅每天供应500名学生用餐,每星期一有A,B两种菜可供选择。调查表明,凡是在这星期一选A菜的,下星期一会有 改选B菜;而选B菜的,下星期一会有
改选B菜;而选B菜的,下星期一会有 改选A菜。用
改选A菜。用 分别表示第
分别表示第 个星期选A的人数和选B的人数.
个星期选A的人数和选B的人数.
⑴试用 表示
表示 ,判断数列
,判断数列 是否成等比数列并说明理由;
是否成等比数列并说明理由;
⑵若第一个星期一选A神菜的有200人,那么第10个星期一选A种菜的大约有多少人?
已知向量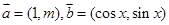 ,函数
,函数 .
.
⑴设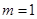 ,x为某三角形的内角,求
,x为某三角形的内角,求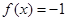 时x的值;
时x的值;
⑵设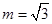 ,当函数
,当函数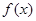 取最大值时,求cos2x的值.
取最大值时,求cos2x的值.