(本小题满分12分)
右图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人
(I)求该专业毕业总人数N和90~95分数段内的人数 ;
;
(II)现欲将90~95分数段内的 名毕业生分配往甲、乙、丙三所学校,若向学校甲分配两名毕业生,且其中至少有一名男生的概率为
名毕业生分配往甲、乙、丙三所学校,若向学校甲分配两名毕业生,且其中至少有一名男生的概率为 ,求
,求 名毕业生中男女各几人(男女人数均至少两人)?
名毕业生中男女各几人(男女人数均至少两人)?
(III)在(II)的结论下,设随机变量 表示n名毕业生中分配往乙学校的三名学生中男生的人数,求
表示n名毕业生中分配往乙学校的三名学生中男生的人数,求 的分布列和数学期望.
的分布列和数学期望.
 如图1:等边
如图1:等边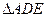 可以看作由等边
可以看作由等边 绕顶点
绕顶点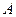 经过旋转相似变换得到.但是我们注意到图形中的
经过旋转相似变换得到.但是我们注意到图形中的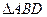 和
和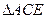 的关系,上述变换也可以理解为图形是由
的关系,上述变换也可以理解为图形是由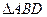 绕顶点
绕顶点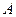 旋转
旋转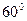 形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转
形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转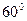 形成的.
形成的.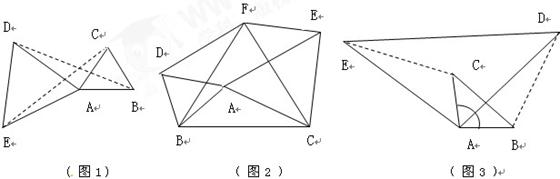
① 利用上述结论解决问题:如图2, 中,
中,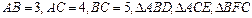 都是等边三角形,求四边形
都是等边三角形,求四边形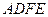 的面积;
的面积;
② 图3中,  ∽
∽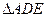 ,
,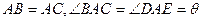 ,仿照上述结论,推广出符合图3的结论.(写出结论即可)
,仿照上述结论,推广出符合图3的结论.(写出结论即可)
已知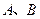 两地相距
两地相距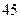 千米,
千米, 骑车人与客车分别从
骑车人与客车分别从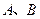 两地出发,往返于
两地出发,往返于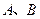 两地之间.下图中,折线表示某骑车人离开
两地之间.下图中,折线表示某骑车人离开 地的距离
地的距离 与时间
与时间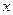 的函数关系.客车
的函数关系.客车 点从
点从 地出发,以
地出发,以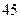 千米/时的速度匀速行驶.(乘客上、下车停车时间忽略不计)
千米/时的速度匀速行驶.(乘客上、下车停车时间忽略不计) 
① 在阅读下 图的基础上,直接回答:
图的基础上,直接回答: 骑车人共休息几次?骑车人总共骑行多少千米?骑车人与客车总共相遇几次?
骑车人共休息几次?骑车人总共骑行多少千米?骑车人与客车总共相遇几次?
② 试问:骑车人何时与客车第二次相遇?(要求写 出演算过程).
出演算过程).
(本小题12分)
已知函数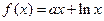
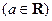 .
.
(Ⅰ)若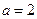 ,求曲线
,求曲线 在
在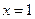 处切线的斜率;
处切线的斜率;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设 ,若对任意
,若对任意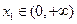 ,均存在
,均存在 ,使得
,使得 ,求
,求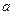 的取值范围。
的取值范围。
(本小题12分)
如图, <
< <
<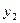 <…<
<…< )是曲线C
)是曲线C
 :
: 上的n个点,点
上的n个点,点 在x轴的正半轴上,且⊿
在x轴的正半轴上,且⊿ 是正三角形(
是正三角形( 是坐标原点)。
是坐标原点)。
(1)写出
(2)求出点 的横坐标
的横坐标 关于n的表达式并用数学归纳法证明
关于n的表达式并用数学归纳法证明
(本小题12分)
某造船公司年造船量是20艘,已知造船 艘的产值函数为
艘的产值函数为 (单位:万元),成本函数为
(单位:万元),成本函数为 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数 的边际函数
的边际函数 定义为
定义为 。
。
(Ⅰ)求利润函数 及边际利润函数
及边际利润函数 ;(提示:利润
;(提示:利润 =产值-成本)
=产值-成本)
(Ⅱ)问年造船量安排多少艘时,可使公司造船的年利润最大?
(Ⅲ)求边际利润函数 单调递减时
单调递减时 的取值范围。
的取值范围。