(本题满分14分)本题共2小题,第(1)小题8分,第(2)小题6分.
如图,摩天轮上一点 在
在 时刻距离地面高度满足
时刻距离地面高度满足 ,
, ,已知某摩天轮的半径为
,已知某摩天轮的半径为 米,点
米,点 距地面的高度为
距地面的高度为 米,摩天轮做匀速转动,每
米,摩天轮做匀速转动,每 分钟转一圈,点
分钟转一圈,点 的起始位置在摩天轮的最低点处.
的起始位置在摩天轮的最低点处.
(1)根据条件写出 (米)关于
(米)关于 (分钟)的解析式;
(分钟)的解析式;
(2)在摩天轮转动的一圈内,有多长时间点 距离地面超过
距离地面超过 米?
米?
(本小题满分14分)(注意:在试题卷上作答无效)
已知曲线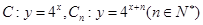 ,从
,从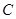 上的点
上的点 作
作 轴的垂线,交
轴的垂线,交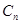 于点
于点 ,再从点
,再从点 作
作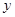 轴的垂线,交
轴的垂线,交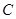 于点
于点 ,设
,设
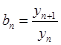
(1)求数列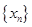 的通项公式;
的通项公式;
(2)记 ,数列
,数列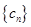 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小
的大小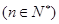 ;
;
(3)记 ,数列
,数列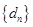 的前
的前 项和为
项和为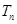 ,试证明:
,试证明:

(本小题14分,计入总分)
已知数列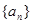 满足:
满足: 
⑴求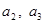 ;
;
⑵当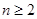 时,求
时,求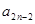 与
与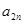 的关系式,并求数列
的关系式,并求数列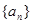 中偶数项的通项公式;
中偶数项的通项公式;
⑶求数列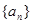 前100项中所有奇数项的和.
前100项中所有奇数项的和.
(本小题满分13分)已知平面上三个向量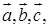 的模均为1,它们相互之间的夹角均为
的模均为1,它们相互之间的夹角均为 。
。
(I)求证: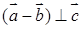 ;
;
(II)若
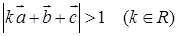 ,求
,求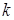 的取值范围。
的取值范围。
(本小题满分12分)
已知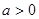 ,函数
,函数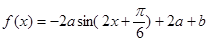 ,
, 时,
时,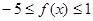 ,求常数
,求常数 ,
,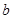 的值.
的值.
(本小题满分12分)
.已知函数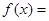
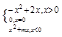 是奇函数.
是奇函数.
(1)求实数 的值;
的值;
(2)若函数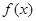 在区间
在区间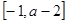 上单调递增,求实数
上单调递增,求实数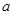 的取值范围.
的取值范围.