(本小题满分12分,(1)小问3分,(2)小问4分,(3)小问5分)
对于函数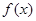 ,若存在实数对(
,若存在实数对(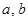 ),使得等式
),使得等式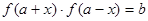 对定义域中的每一个
对定义域中的每一个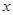 都成立,则称函数
都成立,则称函数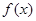 是“(
是“(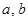 )型函数”.
)型函数”.
(1)判断函数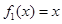 是否为 “(
是否为 “(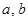 )型函数”,并说明理由;
)型函数”,并说明理由;
(2)若函数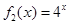 是“(
是“(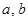 )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对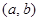 ;
;
(3)已知函数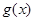 是“(
是“(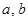 )型函数”,对应的实数对
)型函数”,对应的实数对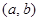 为(1,4).当
为(1,4).当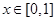 时,
时,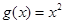
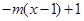
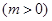 ,若当
,若当 时,都有
时,都有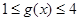 ,试求
,试求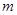 的取值范围.
的取值范围.
某车间有10名工人,其中4人仅会车工,3人仅会钳工,另外3人车、钳工都会,现需选出6人完成一件,需要车工、钳工各3人,问有多少种选派方案?
分析:如果先考虑钳工,因有6人会钳工,故有C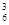 种选法,但此时不清楚选出的钳工中有几个是车钳工都会的,因此也不清楚其余的7人中有多少人会车工,因此在选车工时,就无法确定是从大局出7人中选,还是从6人、5人或4人中选。同样,如果先考虑车工也会遇到同样的问题。因此需对全能工人进行分类:
种选法,但此时不清楚选出的钳工中有几个是车钳工都会的,因此也不清楚其余的7人中有多少人会车工,因此在选车工时,就无法确定是从大局出7人中选,还是从6人、5人或4人中选。同样,如果先考虑车工也会遇到同样的问题。因此需对全能工人进行分类:
(1)选出的6人中不含全能工人;
(2)选出的6人中含有一名全能工人;
(3)选出的6人中含有2名全能工人;
(4)选出的6人中含有31名全能工人;
已知A(-2,0),B(2,0),动点P与A、B两点连线的斜率分别为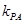 和
和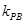 ,且满足
,且满足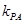 ·
·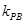 ="t" (t≠0且t≠-1).
="t" (t≠0且t≠-1).
(1)求动点P的轨迹C的方程;
(2)当t<0时,曲线C的两焦点为F1,F2,若曲线C上存在点Q使得∠F1QF2=120°,
求t的取值范围.
已知函数 .
.
(1)将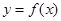 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数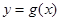 ,求
,求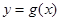 的解析式;
的解析式;
(2)函数 与函数
与函数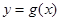 的图像关于直线
的图像关于直线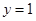 对称,求
对称,求 的解析式;
的解析式;
(3)设
 的最小值是
的最小值是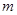 ,且
,且 ,求实数
,求实数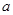 的取值范围.
的取值范围.
求函数 在
在 上的最大值,其中
上的最大值,其中
设函数f(x)=ax2+8x+3 a<0
a<0 。对于给定的负数a,有一个最大的正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5恒成立.问:a为何值时,l(a)最大?求出这个最大的l(a),证明你的结论.
。对于给定的负数a,有一个最大的正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5恒成立.问:a为何值时,l(a)最大?求出这个最大的l(a),证明你的结论.