某商场以每件280元的价格购进一批商品，当每件商品的售价为360元时，每月可售出60件，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出5件．设每件商品的实际售价比原销售价降低了x元．
（1）填表：
（2）要使商场每月销售该商品的利润达到7200元，且更有利于减少库存，则该商品每件实际售价应定为多少元？
学校组织春游，需租用汽车若干辆，如果每辆汽车坐40人，则有20人没有上车；如果每辆汽车坐45人，则可空出一辆汽车，并且有一辆车还可坐10人。问有多少辆汽车？共有多少名学生？
根据要求画图，并回答问题。
已知：直线AB、CD相交于点O，且OE⊥AB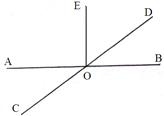
(1)过点O画直线MN⊥CD；
(2)若点F是(1)所画直线MN上任意一点(O点除外)，且∠AOC＝34°，求∠EOF的度数．
如图是由6个同样大小的小正方体搭成的几何体，请你分别画出它的左视图和俯视图．
如图，已知AD=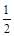
DB，E是BC的中点，BE=
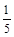AC=2cm，求线段DE的长．
已知：x+y=3，xy=－2，求(3x－4y+2xy)－(2x－5y+5xy)的值．