(本小题满分16分)
在平面直角坐标系xOy中,椭圆C: (a>b>0)的上顶点到焦点的距离为2,离心率为
(a>b>0)的上顶点到焦点的距离为2,离心率为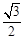 .
.
(1)求a,b的值.
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点.
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值.
(1)写出数列 的前3项;
的前3项;
(2)求数列 的通项公式(写出推证过程);
的通项公式(写出推证过程);
(3)设 ,
, 是数列
是数列 的前
的前 项和,求使得
项和,求使得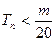 对所有n
对所有n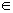 N+都成立的最小正整数
N+都成立的最小正整数 的值。
的值。
(满分13分) 深圳某商场为使销售空调和冰箱获得的总利润达到最大,对即将出售的空调和冰箱相关数据进行调查,得出下表:
| 资金 |
每台空调或冰箱所需资金(百元) |
月资金供应数量 (百元) |
|
| 空调 |
冰箱 |
||
| 成本 |
30 |
20 |
300 |
| 工人工资 |
5 |
10 |
110 |
| 每台利润 |
6 |
8 |
问:该商场怎样确定空调或冰箱的月供应量,才能使总利润最大?
(满分13分)已知数列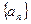 中,
中,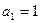 ,
,
(1)判断数列 是否为等比数列?并说明理由;
是否为等比数列?并说明理由;
(2)求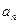
(满分14分)已知不等式 的解集为A,不等式
的解集为A,不等式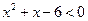 的解集为B。
的解集为B。
(1)求A∩B;
(2)若不等式 的解集为A∩B,求不等式
的解集为A∩B,求不等式 的解集。
的解集。
(满分13分)已知数列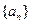 满足
满足 (
(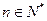 ),它的前
),它的前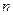 项和为
项和为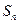 ,且
,且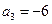 ,
,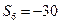 。求数列
。求数列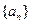 的前
的前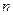 项和的最小值.
项和的最小值.