(满分13分)已知数列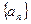 中,
中,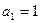 ,
,
(1)判断数列 是否为等比数列?并说明理由;
是否为等比数列?并说明理由;
(2)求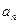
在四棱锥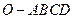 中,底面
中,底面 是边长为1的菱形,
是边长为1的菱形,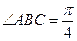 ,
,  底面
底面 ,
,  ,
,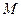 为
为 的中点
的中点
(1)求异面直线AB与MD所成角的大小;
(2)求平面 与平面
与平面 所成的二面角的余弦值.
所成的二面角的余弦值.
设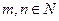 ,
,
 .
.
(1)当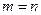 =2011时,记
=2011时,记 ,
,
求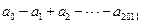 ;
;
(2)若 展开式中
展开式中 的系数是20,则当
的系数是20,则当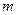 、
、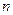 变化时,试求
变化时,试求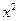 系数的最小值.
系数的最小值.
已知在一个二阶矩阵M的变换作用下, 点 变成了点
变成了点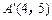 ,点
,点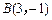 变成了点
变成了点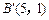 ,求矩阵M.
,求矩阵M.
已知数列a,b,c为各项都是正数的等差数列,公差为d(d>0),在a,b之间和b,c之间共插入m个实数后,所得到的m+3个数所组成的数列{an}是等比数列,其公比为q.
(1)若a=1,m=1,求公差d ;
;
(2)若在a,b之间和b,c之间所插入数的个数均为奇数,求所插入的m数的乘积(用a,c,m表示)
(3)求证:q是无理数.
已知f (x)=ax-ln(-x),x∈(-e,0),g(x)=-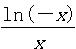 ,其中e是自然常数,a∈R.
,其中e是自然常数,a∈R.
(1)讨论a=-1时, f ( x)的单调性、极值;
x)的单调性、极值;
(2)求证:在(1)的条件下,|f (x)|>g(x)+1/2;
(3)是否存在实数a,使f (x)的最小值是3,如果存在,求出a的值;如果不存在,说明理由.