已知数列a,b,c为各项都是正数的等差数列,公差为d(d>0),在a,b之间和b,c之间共插入m个实数后,所得到的m+3个数所组成的数列{an}是等比数列,其公比为q.
(1)若a=1,m=1,求公差d ;
;
(2)若在a,b之间和b,c之间所插入数的个数均为奇数,求所插入的m数的乘积(用a,c,m表示)
(3)求证:q是无理数.
已知集合A={x|x2﹣x﹣2>0},函数g(x)=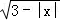 的定义域为集合B,
的定义域为集合B,
(1)求A∩B和A∪B;
(2)若C={x|4x+p<0},且C⊆A,求实数P的取值范围.
已知函数f(x)=ax2+bx+1(a,b∈R且a≠0),F(x)=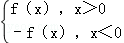 .
.
(1)若f(﹣1)=0,且函数f(x)的值域为[0,+∞),求F(x)的解析式;
(2)在(1)的条件下,当x∈[﹣2,2]时,g(x)=f(x)﹣kx是单调函数,求实数k的取值范围;
(3)设mn<0,m+n>0,a>0,且f(x)是偶函数,判断F(m)+F(n)是否大于零.
二次函数f(x)的图象顶点为A(1,16),且图象在x轴上截得线段长为8.
(1)求函数f(x)的解析式;
(2)令g(x)=(2﹣2a)x﹣f(x);
①若函数g(x)在x∈[0,2]上是单调增函数,求实数a的取值范围;
②求函数g(x)在x∈[0,2]的最小值.
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知函数f(x)=ax2+(b+1)x+b﹣1(a≠0).
(1)当a=1,b=﹣2时,求f(x)的不动点;
(2)若对于任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围.
已知定义域为R的奇函数f(x),当x>0时,f(x)=x2﹣3.
(1)当x<0时,求函数f(x)的解析式;
(2)求函数f(x)在R上的解析式;
(3)解方程f(x)=2x.