柜子里有
双不同的鞋，随机地取出
只，记事件
表示“取出的鞋配不成对”；事件
表示“取出的鞋都是同一只脚的”；事件
表示“取出的鞋一只是左脚的，一只是右脚的，但配不成对”．
（Ⅰ）请列出所有的基本事件；
（Ⅱ）分别求事件、事件、事件的概率．
（本小题满分12分）在△ABC中，角A，B，C的对边分别为a，b，c，且
（1）求
的值；（2）若
，且
，求
的值.
（本小题满分14分）已知函数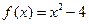
，设曲线y＝f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1,0）（n ÎN *），x1＝4．
（Ⅰ）用
表示xn+1；
（Ⅱ）记an=lg
，证明数列｛an｝成等比数列，并求数列｛xn｝的通项公式；
（Ⅲ）若bn＝xn－2，试比较
与
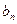的大小．
（本小题满分14分）已知动圆与直线
相切，且过定点F(1, 0)，动圆圆心为M．
（1）求点M的轨迹C的方程；
（2）若直线l与曲线C交于A、B两点，且
（O为坐标原点），求证：直线l过一定点．
（本小题满分14分）如图，在四棱锥
中，底面ABCD是正方形，侧棱
底面ABCD，
，E是PC的中点，作
交PB于点F．
(I) 证明：PA∥平面EDB；
(II) 证明：PB⊥平面EFD；
(III) 求三棱锥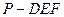
的体积．
（本小题满分14分）设函数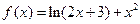
．
（Ⅰ）讨论
的单调性；
（Ⅱ）若
对任意
恒成立，求实数m的取值范围．