(本小题满分14分)已知函数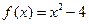 ,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n ÎN *),x1=4.
,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n ÎN *),x1=4.
(Ⅰ)用 表示xn+1;
表示xn+1;
(Ⅱ)记an=lg ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式;
(Ⅲ)若bn=xn-2,试比较 与
与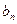 的大小.
的大小.
(本题共3小题,满分18分。第1小题满分4分,第2小题满分7分,第3小题7分)
对定义在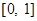 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为 函数.
函数.
① 对任意的 ,总有
,总有 ;
;
② 当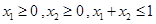 时,总有
时,总有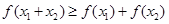 成立.
成立.
已知函数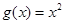 与
与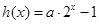 是定义在
是定义在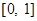 上的函数.
上的函数.
(1)试问函数 是否为
是否为 函数?并说明理由;
函数?并说明理由;
(2)若函数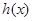 是
是 函数,求实数
函数,求实数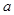 的值;
的值;
(3)在(2)的条件下,是否存在实数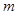 ,使方程
,使方程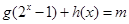 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数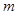 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本题共3小题,满分16分。第1小题满分4分,第2小题满分6分,第3小题6分)
设数列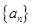 的前
的前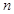 项和为
项和为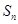 ,若对任意的
,若对任意的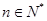 ,有
,有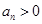 且
且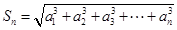 成立.
成立.
(1)求 、
、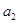 的值;
的值;
(2)求证:数列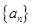 是等差数列,并写出其通项公式
是等差数列,并写出其通项公式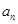 ;
;
(3)设数列 的前
的前 项和为
项和为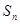 ,令
,令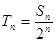 ,若对一切正整数
,若对一切正整数 ,总有
,总有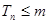 ,求
,求 的取值范围.
的取值范围.
(本题共2小题,满分14分。第1小题满分6分,第2小题满分8分)
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度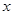 (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到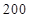 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为 千米/小时;当车流密度不超过
千米/小时;当车流密度不超过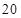 辆/千米时,车流速度为
辆/千米时,车流速度为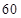 千米/小时,研究表明;当
千米/小时,研究表明;当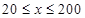 时,车流速度
时,车流速度 是车流密度
是车流密度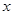 的一次函数.
的一次函数.
(1)求函数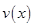 的表达式;
的表达式;
(2)当车流密度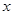 为多大时,车流量(单位时间内通过桥上某一点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某一点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).
(本题共2小题,满分14分。第1小题满分7分,第2小题满分7分)
定义: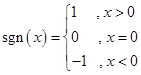 ,若已知函数
,若已知函数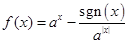 (
(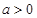 且
且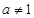 )满足
)满足 .
.
(1)解不等式: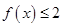 ;
;
(2)若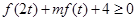 对于任意正实数
对于任意正实数 恒成立,求实数
恒成立,求实数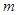 的取值范围.
的取值范围.
(本题共2小题,满分12分。第1小题满分6分,第2小题满分6分)
已知复数 ,
,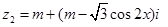 (
( ),且
),且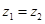 .
.
(1)设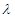 =
=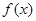 ,求
,求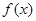 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.
(2)当 时,求函数
时,求函数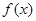 的值域.
的值域.