(本题共3小题,满分18分。第1小题满分4分,第2小题满分7分,第3小题7分)
对定义在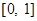 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为 函数.
函数.
① 对任意的 ,总有
,总有 ;
;
② 当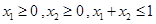 时,总有
时,总有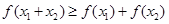 成立.
成立.
已知函数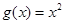 与
与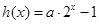 是定义在
是定义在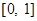 上的函数.
上的函数.
(1)试问函数 是否为
是否为 函数?并说明理由;
函数?并说明理由;
(2)若函数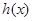 是
是 函数,求实数
函数,求实数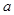 的值;
的值;
(3)在(2)的条件下,是否存在实数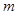 ,使方程
,使方程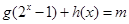 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数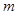 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知向量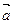 =(1,2),
=(1,2),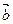 =(cosa,sina),设
=(cosa,sina),设 =
=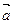 +t
+t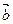 (
( 为实数).
为实数).
(1)若a=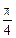 ,求当|
,求当| |取最小值时实数
|取最小值时实数 的值;
的值;
(2)若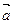 ⊥
⊥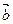 ,问:是否存在实数
,问:是否存在实数 ,使得向量
,使得向量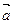 –
–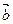 和向量
和向量 的夹角为
的夹角为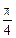 ,若存在,请求出t的值;若不存在,请说明理由.
,若存在,请求出t的值;若不存在,请说明理由.
(3)若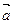 ⊥
⊥ ,求实数
,求实数 的取值范围A,并判断当
的取值范围A,并判断当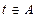 时函数
时函数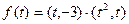 的单调性.
的单调性.
(本小题满分12分)
已知函数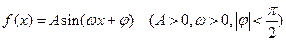 的图象与
的图象与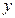 轴的交点为
轴的交点为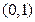 ,它在
,它在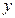 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为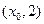 和
和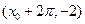 .
.
(1)求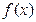 的解析式;
的解析式;
(2)若锐角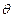 满足
满足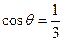 ,求
,求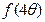 的值.
的值.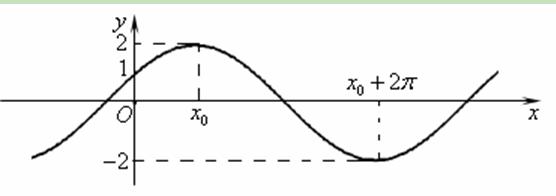
(本小题满分12分)
已知向量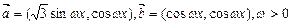 ,记函数
,记函数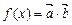 ,
,
若函数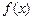 的最小正周期为
的最小正周期为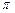 .
.
(1)求 的值;
的值;
(2)当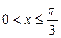 时,试求
时,试求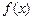 的值域;
的值域;
(3)求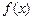 在
在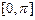 上的单调递增区间.
上的单调递增区间.
(本小题满分12分)在△ABC中, 若I是△ABC的内心, AI的延长线交BC于D, 则有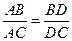 称之为三角形的内角平分线定理, 现已知AC=2, BC=3, AB=4, 且
称之为三角形的内角平分线定理, 现已知AC=2, BC=3, AB=4, 且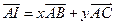 , 求实数
, 求实数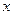 及
及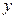 的值.
的值.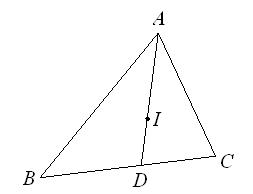
(本小题满分12分)
已知 ,
,
(1)求 和
和 的夹角;
的夹角;
(2)当 取何值时,
取何值时,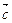 与
与 共线?
共线?
(3)当 取何值时,
取何值时,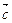 与
与 垂直?
垂直?