已知向量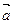 =(1,2),
=(1,2),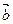 =(cosa,sina),设
=(cosa,sina),设 =
=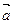 +t
+t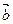 (
( 为实数).
为实数).
(1)若a=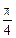 ,求当|
,求当| |取最小值时实数
|取最小值时实数 的值;
的值;
(2)若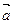 ⊥
⊥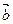 ,问:是否存在实数
,问:是否存在实数 ,使得向量
,使得向量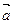 –
–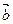 和向量
和向量 的夹角为
的夹角为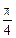 ,若存在,请求出t的值;若不存在,请说明理由.
,若存在,请求出t的值;若不存在,请说明理由.
(3)若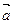 ⊥
⊥ ,求实数
,求实数 的取值范围A,并判断当
的取值范围A,并判断当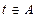 时函数
时函数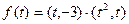 的单调性.
的单调性.
已知数列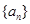 满足
满足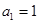 ,
,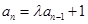 ,
,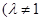 ,
,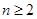 且
且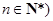 .
.
(1)求证:当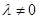 时,数列
时,数列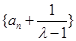 为等比数列;
为等比数列;
(2)如果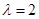 ,求数列
,求数列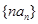 的前
的前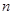 项和
项和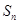 ;
;
(3)如果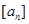 表示不超过
表示不超过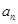 的最大整数,当
的最大整数,当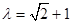 时,求数列
时,求数列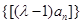 的通项公式.
的通项公式.
已知椭圆 :
: 的右焦点
的右焦点 ,点
,点 在椭圆
在椭圆 上.
上.
(1)求椭圆 的标准方程;
的标准方程;
(2)直线 过点
过点 ,且与椭圆
,且与椭圆 交于
交于 ,
, 两点,过原点
两点,过原点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,如果△
,如果△ 的面积为
的面积为 (
( 为实数),求
为实数),求 的值.
的值.
已知函数 .
.
(1)求函数 的极小值;
的极小值;
(2)如果直线 与函数
与函数 的图象无交点,求
的图象无交点,求 的取值范围.
的取值范围.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2, .
. 
(1)求证:CD⊥平面PAC;
(2)求二面角M-AB-C的大小;
(3)如果N是棱AB上一点,且直线CN与平面MAB所成角的正弦值为 ,求
,求 的值.
的值.
某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为 ,
, ,
, ,
, ,
, .
.
(1)试估计全市学生参加汉字听写考试的平均成绩;
(2)如果从参加本次考试的同学中随机选取1名同学,求这名同学考试成绩在80分以上(含80分)的概率;
(3)如果从参加本次考试的同学中随机选取3名同学,这3名同学中考试成绩在80分以上(含80分)的人数记为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
(注:频率可以视为相应的概率)