如图，一个圆形游戏转盘被分成6个均匀的扇形区域．用力旋转转盘-优题课

如图，一个圆形游戏转盘被分成6个均匀的扇形区域．用力旋转转盘，转盘停止转动时，箭头A所指区域的数字就是每次游戏所得的分数（箭头指向两个区域的边界时重新转动），且箭头A指向每个区域的可能性都是相等的．在一次家庭抽奖的活动中，要求每个家庭派一位儿童和一位成人先后各转动一次游戏转盘，得分记为（假设儿童和成人的得分互不影响，且每个家庭只能参加一次活动）．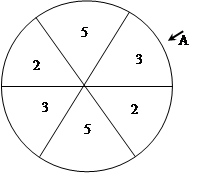

（Ⅰ）请列出一个家庭得分的所有情况；
（Ⅱ）若游戏规定：一个家庭的总得分为参与游戏的两人所得分数之和，且总得分为偶数的家庭可以获得一份奖品．请问一个家庭获奖的概率为多少？