如图, 为△
为△ 外接圆的切线,
外接圆的切线,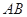 的延长线交直线
的延长线交直线 于点
于点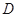 ,
, 分别为弦
分别为弦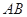 与弦
与弦 上的点,且
上的点,且 ,
,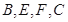 四点共圆.
四点共圆. 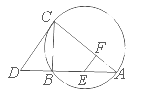
(Ⅰ)证明: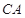 是△
是△ 外接圆的直径;
外接圆的直径;
(Ⅱ)若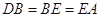 ,求过
,求过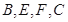 四点的圆的面积与△
四点的圆的面积与△ 外接圆面积的比值.
外接圆面积的比值.
设各项为正的数列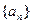 ,其前
,其前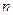 项和为
项和为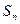 ,并且对所有正整数
,并且对所有正整数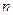 ,
,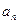 与2的等差中项等于
与2的等差中项等于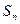 与2的等比中项.
与2的等比中项.
(1)写出数列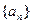 的前二项;
的前二项;
(2)求数列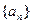 的通项公式(写出推证过程);
的通项公式(写出推证过程);
(3)令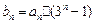 ,求
,求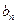 的前
的前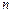 项和
项和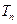 .
.
在△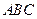 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为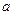 、
、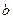 、
、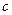 .且
.且 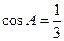 .
.
(1)求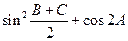 的值;
的值;
(2)若 ,求
,求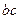 的最大值.
的最大值.
要将两种厚度、材质相同,大小不同的钢板截成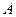 、
、 、
、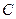 三种规格的成品.每
三种规格的成品.每
张钢板可同时截得三种规格的块数如下表:
| 成品规格类型 钢板类型 |
A规格 |
B规格 |
C规格 |
| 第一种钢板 |
1 |
2 |
1 |
| 第二种钢板 |
1 |
1 |
3 |
每张钢板的面积:第一张为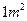 ,第二张为
,第二张为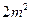 .今需要
.今需要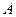 、
、 、
、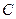 三种规格的成品各为12、15、27块.则两种钢板各截多少张,可得所需三种规格的成品,且使所用钢板的面积最少?
三种规格的成品各为12、15、27块.则两种钢板各截多少张,可得所需三种规格的成品,且使所用钢板的面积最少?
已知函数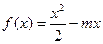 ,其中
,其中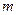 为实常数.
为实常数.
(1)当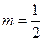 时,求不等式
时,求不等式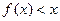 的解集;
的解集;
(2)当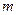 变化时,讨论关于
变化时,讨论关于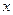 的不等式
的不等式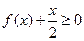 的解集.
的解集.
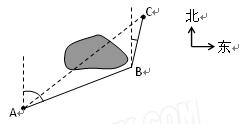
如图,A、C两岛之间有一片暗礁,一艘小船于某日上午8时从A岛出发,以10
海里/小时的速度,沿北偏东75°方向直线航行,下午1时到达B处.然后以同样的速度,
沿北偏东15°方向直线航行,下午4时到达C岛.
(1)求A、C两岛之间的直线 距离;
距离;
(2)求∠BAC的正弦值.