选修4—4:坐标系与参数方程
在平面直角坐标系xOy中,直线l的参数方程为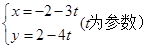 它与曲线C:
它与曲线C: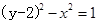 交于A、B两点。
交于A、B两点。
(1)求|AB|的长
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为 ,求点P到线段AB中点M的距离。
,求点P到线段AB中点M的距离。
若x,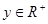 ,且
,且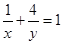 ,求u=x+y的最小值.
,求u=x+y的最小值.
已知数列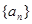 满足:
满足: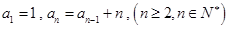 .
.
(Ⅰ)求数列的通项公式;
(Ⅱ)设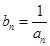 ,求数列
,求数列 的前
的前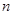 项和
项和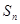 .
.
某开发商用9000万元在市区购买一块土地建一幢写字楼,规划要求写字楼每层建筑面积为2000平方米.已知该写字楼第一层的建筑费用为每平方米4000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加100元.
(1)若该写字楼共x层,总开发费用为y万元,求函数y=f(x)的表达式;(总开发费用=总建筑费用+购地费用)
(2)要使整幢写字楼每平方米的平均开发费用最低,该写字楼应建为多少层?
变量x、y满足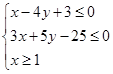
(1)设z=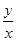 ,求z的最小值;
,求z的最小值;
(2)设z=x2+y2,求z的取值范围.
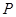 为椭圆
为椭圆 上任意一点,
上任意一点,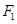 、
、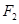 为左右焦点.如图所示:
为左右焦点.如图所示: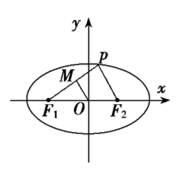
(1)若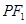 的中点为
的中点为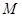 ,求证
,求证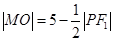 ;
;
(2)若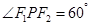 ,求
,求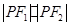 的值.
的值.