函数 ,
, (其中
(其中 ,
, ,
, )的图象与
)的图象与 轴相邻两个交点之间的距离为,且图象上一个最低点为
轴相邻两个交点之间的距离为,且图象上一个最低点为 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)求 的单调递增区间;
的单调递增区间;
(Ⅲ)当 时,求
时,求 的值域.
的值域.
(本小题满分13分)
在某校组织的一次篮球定点投篮比赛中,两人一对一比赛规则如下:若某人某次投篮命中,则由他继续投篮,否则由对方接替投篮. 现由甲、乙两人进行一对一投篮比赛,甲和乙每次投篮命中的概率分别是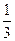 ,
,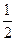 .两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
.两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
(Ⅰ)求3次投篮的人依次是甲、甲、乙的概率;
(Ⅱ)若投篮命中一次得1分,否则得0分. 用ξ表示甲的总得分,求ξ的分布列和数学期望.
(本小题满分13分)在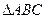 中,角
中,角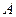 ,
,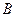 ,
,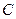 所对的边分别为
所对的边分别为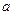 ,
, ,
,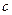 ,且
,且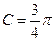 ,
,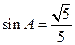 .
.
(Ⅰ)求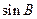 的值;
的值;
(Ⅱ)若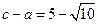 ,求
,求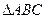 的面积.
的面积.
设集合W由满足下列两个条件的数列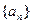 构成:
构成:
①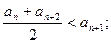
②存在实数M,使 (n为正整数)
(n为正整数)
(I)在只有5项的有限数列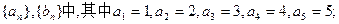
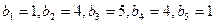 ;试判断数列
;试判断数列 是否为集合W的元素;
是否为集合W的元素;
(II)设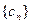 是各项为正的等比数列,
是各项为正的等比数列, 是其前n项和,
是其前n项和,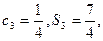 证明数列
证明数列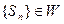 ;并写出M的取值范围;
;并写出M的取值范围;
(III)设数列 且对满足条件的M的最小值M0,都有
且对满足条件的M的最小值M0,都有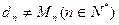 .
.
求证:数列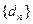 单调递增.
单调递增.
在直角坐标系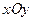 中,点M到点
中,点M到点 的距离之和是4,点M的轨迹是C与x轴的负半轴交于点A,不过点A的直线
的距离之和是4,点M的轨迹是C与x轴的负半轴交于点A,不过点A的直线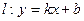 与轨迹C交于不同的两点P和Q.
与轨迹C交于不同的两点P和Q.
(I)求轨迹C的方程;
(II)当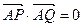 时,求k与b的关系,并证明直线
时,求k与b的关系,并证明直线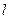 过定点.
过定点.
已知函数
(I)当a<0时,求函数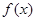 的单调区间;
的单调区间;
(II)若函数f(x)在[1,e]上的最小值是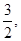 求a的值.
求a的值.