设集合W由满足下列两个条件的数列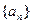
构成：
①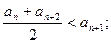
②存在实数M，使
（n为正整数）
（I）在只有5项的有限数列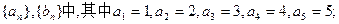
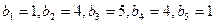；试判断数列
是否为集合W的元素；
（II）设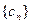
是各项为正的等比数列，
是其前n项和，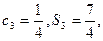
证明数列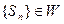
；并写出M的取值范围；
（III）设数列
且对满足条件的M的最小值M0，都有
.
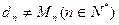求证：数列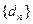
单调递增.
（本小题满分12分）
图1是某种称为“凹槽”的机械部件的示意图，图2是凹槽的横截面（阴影部分）示意图，其中四边形ABCD是矩形，弧CmD是半圆，凹槽的横截面的周长为4.已知凹槽的强度与横截面的面积成正比，比例系数为
,设AB=2x,BC=y.（Ⅰ）写出y关于x函数表达式，并指出x的取值范围；（Ⅱ）求当x取何值时，凹槽的强度最大.
已知
是三角形
三内角，向量
，且
．（1）求角
；（2）若
，求
的值。
(本小题满分13分)
已知函数
．(Ⅰ)当
时，求
的最小正周期和值域；(Ⅱ)若函数在区间
上是增函数，求实数
的取值范围．
已知函数
,数列
满足
．
(Ⅰ)求证：数列
是等差数列；(Ⅱ)记
,试比较
与1的大小.
设平面直角坐标系
中，设二次函数
的图象与两坐标轴有三个交点，经过这三个交点的圆记为C．求：（Ⅰ）求实数b 的取值范围；（Ⅱ）求圆C 的方程，并写出圆C上必过的定点坐标；