已知在一个二阶矩阵M的变换作用下, 点 变成了点
变成了点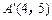 ,点
,点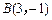 变成了点
变成了点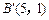 ,求矩阵M.
,求矩阵M.
(请考生在第22、23两题中任选一题作 答,如果多做。则按所做的第一题记分.
答,如果多做。则按所做的第一题记分.
(本小题满分10分)选修4-1:几何证明选讲
如图:AB是⊙O的直径,G是AB延长线上的一点,GCD是⊙O的割线,过点G作AG的垂线,交直线AC于点E,交直线AD于点F,过点G作⊙O的切线,切点为H.求证:
(Ⅰ)C、D、F、E四点共圆;
(Ⅱ)GH2=GE·GF.
(本小题满分12分)
已知函数f(x)=a -x-lnx(a∈R).
-x-lnx(a∈R).
(Ⅰ)求函数f(x)的单调区 间;
间;
(Ⅱ)当a=1时,证明:(x-1)( lnx-f(x))≥0.
lnx-f(x))≥0.
((本小题满分12分)
在平面直角坐标系xoy中,椭圆E: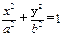 (a>0,b>0)经过点A(
(a>0,b>0)经过点A(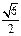 ,
,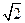 ),且点F(0,-1)为其一个焦点.
),且点F(0,-1)为其一个焦点.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设椭圆E与y轴的两 个交点为A1,A2,不在y轴上的动点P在直线y=b2上运动,直线PA1,PA2分别与椭圆E交于点M,N,证明:直线MN通过一个定点,且△FMN的周长为定值.
个交点为A1,A2,不在y轴上的动点P在直线y=b2上运动,直线PA1,PA2分别与椭圆E交于点M,N,证明:直线MN通过一个定点,且△FMN的周长为定值.
((本小题满分12分)
为了比较两种肥料A、B对同类橘子树产量的影响(此处橘子树的产量是指每一棵橘子树的产量,单位是千克),试验人员分别从施用这两种肥料的橘子树中随机抽取了200棵,其中100棵橘子树施用了A种肥料,另100棵橘子树施用了B种肥料作为样本进行分析,其 中样本橘子树产量的分组区间为[5,15),[15,25),[25,35),[35,45),[45,55),由此得到表1和图1的所示内容,其中表1是施用A种肥料后橘子树产量的频数分布表,图1是施用B种肥料后橘子树产量的频率分布直方图.
中样本橘子树产量的分组区间为[5,15),[15,25),[25,35),[35,45),[45,55),由此得到表1和图1的所示内容,其中表1是施用A种肥料后橘子树产量的频数分布表,图1是施用B种肥料后橘子树产量的频率分布直方图.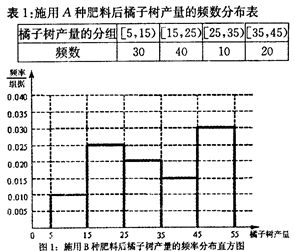
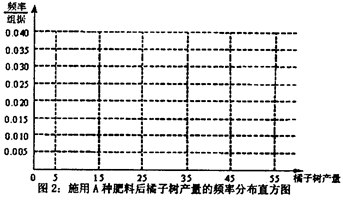
(Ⅰ)完成图2和表2,其中图2是施用A种肥料后橘子树产量的频率分布直方图,表2是施用B种肥料后橘子树产量的频数分布表,并 比较施用A、B两种肥料对橘子树产量提高的影响那种更大,理由是什么?
比较施用A、B两种肥料对橘子树产量提高的影响那种更大,理由是什么?
表2:施用B种肥料后橘子树产量的频数分布表
| 橘子树产量的分组 |
[5,15) |
[15,25) |
[25,35) |
[35,45) |
[45,55) |
| 频数 |
(Ⅱ)把施用了B种肥料的橘子树中产量不低于45千克的橘子树记为甲类橘子树,产量小于15千克的橘子树记为乙类橘子树,现采用分层抽样方法从甲、乙两类橘子树中抽取4棵进行跟踪研究,若从抽得的4棵橘子树中随机抽取2棵进行跟踪研究结果的对比,记X为这两颗橘子树中甲类橘子树的个数,求X的分布列.
(本小题满分12分)
如图:已知△PAB所在的平面与菱形ABCD所在的平面垂直,且PA=PB=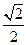 AB,∠ABC=60°,E为AB的中点.
AB,∠ABC=60°,E为AB的中点.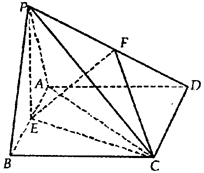
(Ⅰ)证明:CE⊥PA;
(Ⅱ)若F为线段PD上的点,且EF与平面PEC的
夹角为45°,求平面EFC与平面PBC夹角的
余弦值.