已知数列{an}的首项a1=a,Sn是数列{an}的前n项和,且满足: =3n2an+
=3n2an+ ,an≠0,n≥2,n∈N*.
,an≠0,n≥2,n∈N*.
(1)若数列{an}是等差数列,求a的值;
(2)确定a的取值集合M,使a∈M时,数列{an}是递增数列.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
(1)请把字母 标记在正方体相应的顶点处(不需要说明理由)
标记在正方体相应的顶点处(不需要说明理由)
(2)判断平面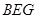 与平面
与平面 的位置关系.并证明你的结论.
的位置关系.并证明你的结论.
(3)证明:直线
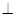 平面
平面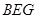
如图,四边形 与四边形
与四边形 都是梯形,
都是梯形, ,
,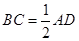 ,
, ,
, ,
, 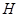 是
是 的中点.
的中点.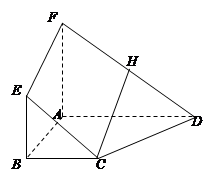
(1)证明: 平面
平面 ;
;
(2)判断 、
、 、
、 、
、 四点是否共面,并说明理由.
四点是否共面,并说明理由.
已知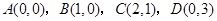 ,将四边形
,将四边形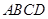 绕
绕 轴旋转一周,求所得旋转体的表面积和体积.
轴旋转一周,求所得旋转体的表面积和体积.
空间四边形ABCD中,AB=CD且AB与CD所成的角为60°,E、F分别是BC、AD的中点,求EF与AB所成角的大小.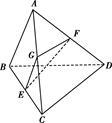
某人上午7:00乘汽车以v1千米/小时(30≤v1≤100)匀速从A地出发到距300公里的B地,在B地不作停留,然后骑摩托车以v2千米/小时(4≤v2≤20)匀速从B地出发到距50公里的C地,计划在当天16:00至21:00到达C地.设乘汽车、骑摩托车的时间分别是x,y小时,如果已知所需的经费P=100+3(5﹣x)+2(8﹣y)元,那么v1,v2分别是多少时走的最经济,此时花费多少元?