已知函数f(x)＝x3＋bx2＋cx＋d在区间[－1,2]上是减函数，那么b＋c（）
A．有最大值 |
B．有最大值－ |
| C．有最小值 |
D．有最小值－ |
若实数x，y满足不等式组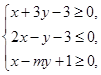
且x＋y的最大值为9，则实数m＝( )
| A．－2 | B．－1 | C．1 | D．2 |
设x，y∈R，a>1，b>1，若ax＝by＝3，a＋b＝
，则
＋
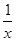的最大值为( )
| A．2 | B． |
C．1 | D． |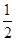
已知三个不等式x2-4x+3＜0…①,x2-6x+8＜0…②,2x2-9x+m＜0…③,要使同时满足①和②的所有x的值都满足③,则实数m的取值范围是（）
| A．m＞9 | B．m＝9 | C．m≤9 | D．0＜m≤9 |
0＜a≤
是函数f(x)＝ax2+2(a-1)x+2在区间(-∞,4］上为减函数的（）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
的公差
，
，且
，
，
成等比数列．
为
项和，则
的值为（ ）
