(本小题满分10分)选修4—4:坐标系与参数方程
已知直线l的参数方程为 (t为参数,m为常数),以直角坐标系xOy的原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为:ρ2-2ρsinθ-4=0,且直线l与圆C交于A、B两点.
(t为参数,m为常数),以直角坐标系xOy的原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为:ρ2-2ρsinθ-4=0,且直线l与圆C交于A、B两点.
(1)若|AB|=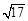 ,求直线l的倾斜角;
,求直线l的倾斜角;
(2)若点P的极坐标为(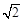 ,
,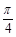 ),且满足2
),且满足2 ,求此时直线l的直角坐标方程.
,求此时直线l的直角坐标方程.
已知数列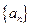 满足对任意的
满足对任意的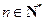 ,都有
,都有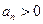 ,
,
且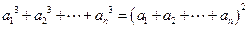 .
.
(1)求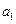 ,
,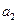 的值;
的值;
(2)求数列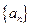 的通项公式
的通项公式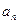 ;
;
(3)设数列 的前
的前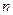 项和为
项和为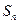 ,不等式
,不等式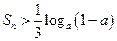 对任意的正整数
对任意的正整数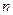 恒成立,求实数
恒成立,求实数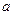 的取值范围.
的取值范围.
已知函数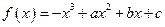 在
在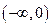 上是减函数,在
上是减函数,在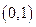 上是增函数,函数
上是增函数,函数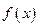 在
在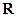 上有三个零点,且1是其中一个零点.
上有三个零点,且1是其中一个零点.
(1)求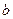 的值;
的值;
(2)求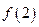 的取值范围;
的取值范围;
(3)试探究直线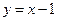 与函数
与函数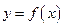 的图像交点个数的情况,并说明理由.
的图像交点个数的情况,并说明理由.
已知动点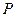 到定点
到定点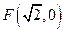 的距离与点
的距离与点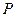 到定直线
到定直线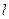 :
: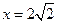 的距离之比为
的距离之比为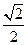 .
.
(1)求动点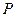 的轨迹
的轨迹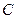 的方程;
的方程;
(2)设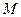 、
、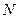 是直线
是直线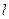 上的两个点,点
上的两个点,点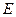 与点
与点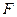 关于原点
关于原点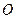 对称,若
对称,若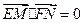 ,求
,求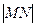 的最小值.
的最小值.
已知直线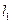 :
: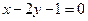 ,直线
,直线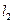 :
: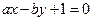 ,其中
,其中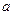 ,
,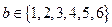 .
.
(1)求直线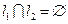 的概率;
的概率;
(2)求直线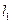 与
与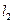 的交点位于第一象限的概率.
的交点位于第一象限的概率.
已知函数 (
( )的最小正周期为
)的最小正周期为 .
.
(Ⅰ)求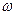 的值;
的值;
(Ⅱ)求函数 在区间
在区间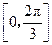 上的取值范围.
上的取值范围.