如图，某居民小区有一朝向为正南方向的居民楼，该居民楼的一楼是高
米的小区超市，超市以上是居民住房，在该楼的前面
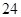米处要盖一栋高
米的新楼．当冬季正午的阳光与水平线的夹角为
时．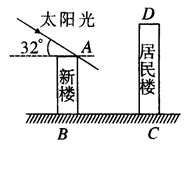
（
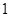）问超市以上的居民住房采光是否有影响，为什么？
（
）若要使超市采光不受影响，两楼应相距多少米？
（参考数据：sin≈
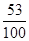，cos≈
≈
．）
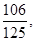
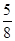全班约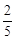
是男生，约
是女生，请根据所给数据完成扇形统计图.
某人将20000元钱分成两部分，按两种不同方式存入银行，其中10000元按活期方式存一年，另10000元按定期存一年，一年后共取回21044元，又已知定期一年存款约利率为0.63％，求活期存款月利率是多少？
肖青的妈妈前年买了某公司的二年期债券4500元，今年到期，扣除利息税后，共得本利和约4700元，问这种债券的年利率是多少？（精确到0.01％）
教育储蓄年利率为1.98％，免征利息税，某企业发行的债券月利率为2.15‰，但要征收20％的利息税，为获取更大回报，投资者应选择哪一种储蓄呢？某人存入28000元，一年到期后可以多收益多少元？
小明的爸爸前年存了年利率为2.25％的二年期定期储蓄，今年到期后，扣除利息税，所得利息正好为小明买以一只价值576元的CD机，问小明爸爸前年存了多少钱？