对甲、乙两种商品重量的误差进行抽查，测得数据如下(单位：mg)：
甲：13 15 14 14 9 14 21 9 10 11
乙：10 14 9 12 15 14 11 19 22 16
(1)画出样本数据的茎叶图，并指出甲、乙两种商品重量误差的中位数；
(2)计算甲种商品重量误差的样本方差；
(3)现从重量误差不低于15的乙种商品中随机抽取2件，求重量误差为19的商品被抽中的概率．
已知函数
(1)求函数
的定义域；
(2)求
的值；
（1）解关于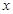
的不等式
；
（2）若关于
的不等式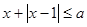
有解，求实数
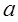的取值范围．
已知直线
的参数方程为
（t为参数），曲线C的参数方程为
（
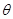为参数）．
（1）已知在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，点P的极坐标为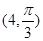
，判断点P与直线的位置关系；
（2）设点Q是曲线C上的一个动点，求点Q到直线的距离的最小值与最大值．
如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E、D，连结EC、CD.
（Ⅰ）求证：直线AB是⊙O的切线；
（Ⅱ）若tan∠CED=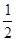
,⊙O的半径为3，求OA的长.
．
；
对一切实数
均成立，求
的取值范围．