(本小题满分14分)已知椭圆 (
(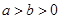 )的左、右顶点分别为
)的左、右顶点分别为 ,
, ,
,
且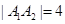 ,
, 为椭圆上异于
为椭圆上异于 ,
, 的点,
的点, 和
和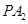 的斜率之积为
的斜率之积为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)设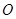 为椭圆中心,
为椭圆中心, ,
, 是椭圆上异于顶点的两个动点,求
是椭圆上异于顶点的两个动点,求 面积的最大值.
面积的最大值.
设函数 (1)当
(1)当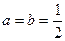 时,求
时,求 的最大值;(2)令
的最大值;(2)令 ,(0
,(0 ≤3),其图象上任意一点
≤3),其图象上任意一点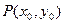 处切线的斜率
处切线的斜率 ≤
≤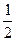 恒成立,求实数
恒成立,求实数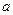 的取值范围;(3)当
的取值范围;(3)当 ,
, ,方程
,方程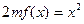 有唯一实数解,求正数
有唯一实数解,求正数 的值。
的值。
已知平面 上的动点
上的动点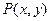 及两定点A(-2,0),B(2,0),直线PA,PB的斜率分别是
及两定点A(-2,0),B(2,0),直线PA,PB的斜率分别是 ,
, ,且
,且 ·
·
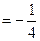 。(1)求动点P的轨迹C的方程;
。(1)求动点P的轨迹C的方程;
(2)已知直线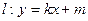 与曲线C交于M,N两点,且直线BM,BN的斜率都存在并满足
与曲线C交于M,N两点,且直线BM,BN的斜率都存在并满足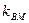 ·
·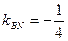 ,求证:直线
,求证:直线 过原点。
过原点。
已知,等差数列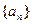 的首项
的首项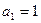 ,公差
,公差 ,且第二项、第五项、第十四项分别是等比数列
,且第二项、第五项、第十四项分别是等比数列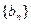 的第二项、第三项、第四项。(1)求数列
的第二项、第三项、第四项。(1)求数列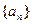
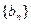 的通项公式;(2)设数列
的通项公式;(2)设数列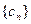 对任意正整数
对任意正整数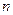 均有
均有 成立,求数列
成立,求数列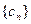 的前
的前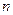 项的和
项的和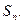
某校积极响应《全面健身条例》,把周五下午5:0 0~6:00定为职工活动时间,并成立了行政和教师两支篮球队,但由于工作性质所限,每月(假设为4周)每支球队只能组织两次活动,且两支球队的活动时间是相互独立的。
0~6:00定为职工活动时间,并成立了行政和教师两支篮球队,但由于工作性质所限,每月(假设为4周)每支球队只能组织两次活动,且两支球队的活动时间是相互独立的。
(1)求这两 支球队每月两次都在同一时间活动的频率;
支球队每月两次都在同一时间活动的频率;
(2)设这两支球队每月能同时活动的次数为 ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。
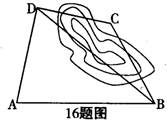 如图,为了计算渭河岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测得AD⊥CD,AD=100m,AB=140m,∠BDA=60°,∠BCD=135°,求两景点B与C的距离(假设A,B,C,D在同一平面内,测量结果保留整数;参考数据:
如图,为了计算渭河岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测得AD⊥CD,AD=100m,AB=140m,∠BDA=60°,∠BCD=135°,求两景点B与C的距离(假设A,B,C,D在同一平面内,测量结果保留整数;参考数据: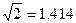 ,
, ,
, .)
.)