本题共有 3 个小题,第 1 小题满分 3 分,第 2 小题满分4分,第 3 小题满分5分.
已知抛物线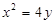 ,过原点作斜率为1的直线交抛物线于第一象限内一点
,过原点作斜率为1的直线交抛物线于第一象限内一点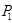 ,又过点
,又过点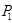 作斜率为
作斜率为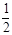 的直线交抛物线于点
的直线交抛物线于点 ,再过
,再过 作斜率为
作斜率为 的直线交抛物线于点
的直线交抛物线于点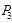 ,
, ,如此继续。一般地,过点
,如此继续。一般地,过点 作斜率为
作斜率为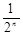 的直线交抛物线于点
的直线交抛物线于点 ,设点
,设点 .
.
(1)求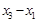 的值;
的值;
(2)令 ,求证:数列
,求证:数列 是等比数列;
是等比数列;
(3)记 为点列
为点列 的极限点,求点
的极限点,求点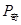 的坐标.
的坐标.
(本小题满分12分)在△ABC中,已知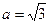 ,
, ,
,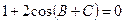 ,
,
求(1)角A,B ; (2)求BC边上的高。
(本小题满分12分)
(1)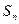 为等差数列{an}的前n项和,
为等差数列{an}的前n项和,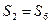 ,
,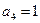 ,求
,求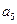 .
.
(2)在等比数列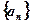 中,若
中,若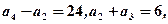 求首项
求首项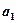 和公比
和公比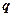 。
。
(本小题满分14分)已知集合 是满足下列性质的函数
是满足下列性质的函数 的全体:对于定义域B中的任何两个自变量
的全体:对于定义域B中的任何两个自变量 ,都有
,都有 。(1)当B=R时,
。(1)当B=R时, 是否属于
是否属于 ?为什么?(2)当B=
?为什么?(2)当B= 时,
时, 是否属于
是否属于 ,若属于请给予证明;若
,若属于请给予证明;若
不属于说明理由,并说明是否存在一个 使
使 属于
属于 ?
?
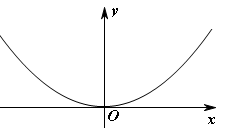
(文)(本小题满分12分)已知y=f(x)是偶函数,当x>0时,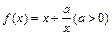 ,
,
且当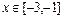 时,
时,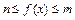 恒成立,若a≥9,求
恒成立,若a≥9,求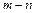 的最小值.
的最小值.
(理)(本小题满分12分)已知y=f(x)是偶函数,当x>0时,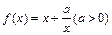 ,
,
且当 时,
时, 恒成立,求
恒成立,求 的最小值.
的最小值.