(本小题满分13分)为了加强环保建设,提高社会效益和经济效益,某市计划用若干年时间更换10000辆燃油型公交车。每更换一辆新车,则淘汰一辆旧车,更换的新车为电力型车和混合动力型车。今年初投入了电力型公交车 辆,混合动力型公交车
辆,混合动力型公交车 辆,计划以后电力型车每年的投入量比上一年增加
辆,计划以后电力型车每年的投入量比上一年增加 ,混合动力型车每年比上一年多投入
,混合动力型车每年比上一年多投入 辆.设
辆.设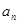 、
、 分别为第
分别为第 年投入的电力型公交车、混合动力型公交车的数量,设
年投入的电力型公交车、混合动力型公交车的数量,设 、
、 分别为
分别为 年里投入的电力型公交车、混合动力型公交车的总数量。
年里投入的电力型公交车、混合动力型公交车的总数量。
(1)求 、
、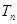 ,并求
,并求 年里投入的所有新公交车的总数
年里投入的所有新公交车的总数 ;
;
(2)该市计划用 年的时间完成全部更换,求
年的时间完成全部更换,求 的最小值.
的最小值.
如图在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,过D与PB垂直的平面分别交PB、PC于F、E。PD=DC。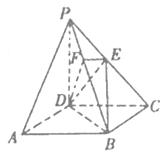
(1)求证:DE⊥PC
(2)求证:PA//平面EDB;
(3)求二面角C—PB—D的大小。
已知函数 时取最大值2。
时取最大值2。 是集合
是集合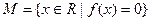 中的任意两个元素,
中的任意两个元素,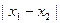 的最小值为。
的最小值为。
(1)求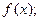

(2)若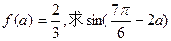 的值。
的值。
过点P(-2,-3)作圆C:(x-4)2+(y-2)2=9的两条切线,切点分别为A、B.求:
(1)经过圆心C,切点A、B这三点的圆的方程;
(2)直线AB的方程;
(3)线段AB的长.
圆心在直线5x-3y-8=0上的圆与两坐标轴相切,求此圆的方程.
求过直线2x+y+4=0和圆x2+y2+2x-4y+1=0的交点,且满足下列条件之一的圆的方程.
(1)过原点;
(2)有最小面积.