(本小题满分12分)已知各项不为零的数列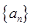 的前
的前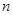 项和为
项和为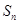 ,且满足
,且满足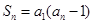 .
.
(1)求数列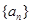 的通项公式;
的通项公式;
(2)设数列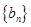 满足
满足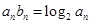 ,求数列
,求数列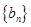 的前
的前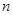 项和
项和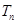 .
.
(本小题满分12分)
已知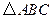 中,角
中,角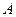 、
、 、
、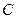 所对的边分别为
所对的边分别为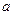 、
、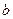 、
、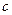 ,
,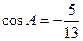 ,
,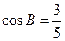 .
.
(1)求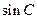 的值;
的值;
(2)若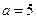 ,求
,求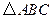 的面积.
的面积.
(本小题满分16分) 一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j).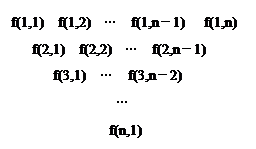
(1)若数表中第i (1≤i≤n-3)行的数依次成等差数列,求证:第i+1行的数也依次成等差数列;
(2)已知f(1,j)=4j,求f(i,1)关于i的表达式;
(3)在(2)的条件下,若f(i,1)=(i+1)(ai-1),bi= ,试求一个函数g(x),使得
Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当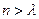 时,都有Sn >m.
时,都有Sn >m.
(本小题满分16分)某厂生产某种产品的年固定成本为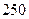 万元,每生产
万元,每生产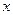 (
(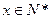 )千件,需另投入成本为
)千件,需另投入成本为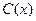 ,当年产量不足
,当年产量不足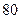 千件时,
千件时,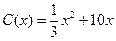 (万元);当年产量不小于
(万元);当年产量不小于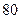 千件时,
千件时,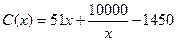 (万元).通过市场分析,若每千件售价为
(万元).通过市场分析,若每千件售价为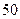 万元时,该厂年内生产该商品能全部销售完.
万元时,该厂年内生产该商品能全部销售完.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量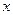 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大.
(本小题满分15分)如图,斜三棱柱ABC—A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角.
(1)求证:AC⊥面ABC1;
(2)求证:C1点在平面ABC上的射影H在直线AB上;
(3)求此三棱柱体积的最小值.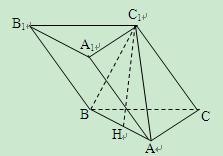
(本小题满分15分)已知公差大于零的等差数列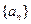 的前n项和为Sn,且满足:
的前n项和为Sn,且满足: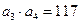 ,
,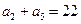 .
.
(1)求数列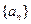 的通项公式
的通项公式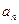 ;
;
(2)若数列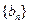 是等差数列,且
是等差数列,且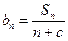 ,求非零常数c.
,求非零常数c.